Page 18 - Toán 9 - GV Đỗ Đạt

0
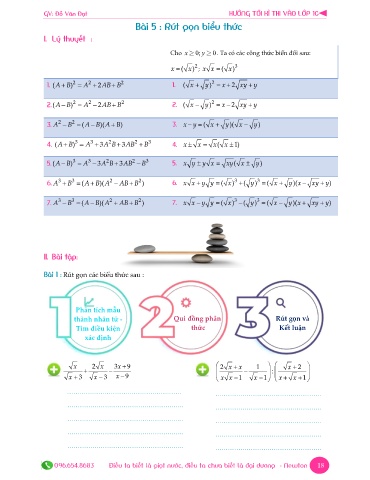
Cho x  0; y  . Ta có các công thức biến đổi sau:
3
2
x  ( x ) ; x x  ( x )
2
2
2
y
(A B )  A  2AB B ( x  ) y 2  x  2 xy 

2
2
2

(A B )  A  2AB B ( x  ) y 2  x  2 xy  y
2
2
)


A  B  (A B )(A B x y  ( x  y )( x  ) y
2
2
3
3
3
(A B )  A  3A B 3AB  B x  x  ( x x  1)
2
2
3
3
3
(A B )  A  3A B 3AB  B x y  y x  xy ( x  ) y
3
3
2
3
3

A  B  (A B )(A  AB B 2 ) x x  y y  ( x )  ( y )  ( x  y )(x  xy  ) y

3
3
3
2
3

A  B  (A B )(A  AB B 2 ) x x  y y  ( x )  ( y )  ( x  y )(x  xy  ) y


Rút gọn các biểu thức sau :

Phân tích mẫu
thành nhân tử - Qui đồng phân Rút gọn và
Tìm điều kiện thức Kết luận
xác định

x  2 x  3x  9  2 x x 1   x  2 

:  


x  3 x  3 x  9  x x  1  x  1   x  x  1 
 



………………………………………………. ……………………………………………
……………………………………………….. ……………………………………………
……………………………………………….. ……………………………………………
……………………………………………….. ……………………………………………

……………………………………………….. ……………………………………………

18