Page 68 - ISCI’2017

t ! n
∑ = 2048 , − kn = 12,
= i 0 i ( ! n −i )!
i.e. the relative speed (25) is also equal to 1.
Unfortunately, in the works [53 – 54] was been shown, any non-trivial perfect code has the

parameters of the Hamming’s code or Golay’s code, i.e. an achieving maximum relative speed the

Niederreiter scheme limits only these schemes (constructions). The most another codes, includes the
Goppa codes, have the design (n, k, d)-parameters, lying considerably below the upper border (26)

(real distance characteristics of the Goppa codes are higher). For example, for the Goppa codes with
the parameters n = 1024, k = 524, t = 50 (used in the author's version [15] of the McEliece scheme)

*
the relative speed encryption (24) in the Niederreiter scheme is equal to R ≈ 0,57, which is
unsubstantially greater compared to the speed R ≈ 0,51 the McEliece scheme. Since the code length
*
increases the design parameters of the Goppa code are deteriorating, which leads to a speed reduction
*
R . This tendency is clearly shown the calculation results in Table 2, which has assessments of the
relative speed of data transmission for the McEliece and Niederreiter cryptosystems at using the codes
with the parameters from Table 1.

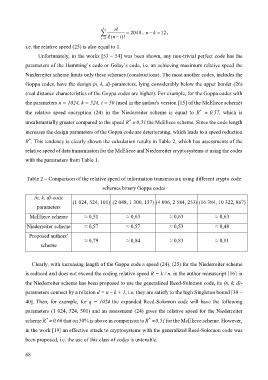
Table 2 – Comparison of the relative speed of information transmission using different crypto code

schemes binary Goppa codes

(n, k, d)-code
(1 024, 524, 101) (2 048, 1 300, 137) (4 096, 2 584, 253) (16 384, 10 322, 867)
parameters

McEliece scheme ≈ 0,51 ≈ 0,63 ≈ 0,63 ≈ 0,63

Niederreiter scheme ≈ 0,57 ≈ 0,57 ≈ 0,53 ≈ 0,48
Proposed authors’
≈ 0,79 ≈ 0,84 ≈ 0,83 ≈ 0,81
scheme

Clearly, with increasing length of the Goppa code a speed (24), (25) for the Niederreiter scheme

is reduced and does not exceed the coding relative speed R = k / n. in the author manuscript [16] in
the Niederreiter scheme has been proposed to use the generalized Reed-Solomon code, its (n, k, d)-

parameters connect by a relation d = n – k + 1, i.e. they are satisfy to the high Singleton bound [38 –
40]. Then, for example, for q = 1024 the expanded Reed-Solomon code will have the following

parameters (1 024, 524, 501) and an assessment (24) gives the relative speed for the Niederreiter

*
*
scheme R ≈ 0,66 that on 30% is above in comparison to R ≈ 0,51 for the McEliece scheme. However,
in the work [19] an effective attack to cryptosystems with the generalized Reed-Solomon code was
been proposed, i.e. the use of this class of codes is untenable.

68