Page 48 - 091math-wb-w3-(sets)

WORKBOOK

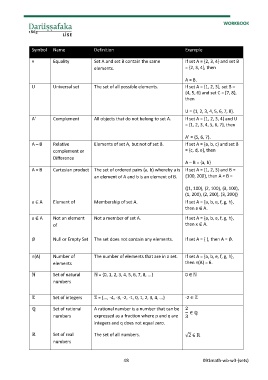
Symbol Name Definition Example

= Equality Set A and set B contain the same If set A = {2, 3, 4} and set B
elements. = {2, 3, 4}, then

A = B.
U Universal set The set of all possible elements. If set A = {1, 2, 3}, set B =
{4, 5, 6} and set C = {7, 8},
then

U = {1, 2, 3, 4, 5, 6, 7, 8}.
A’ Complement All objects that do not belong to set A. If set A = {1, 2, 3, 4} and U
= {1, 2, 3, 4, 5, 6, 7}, then

A’ = {5, 6, 7}.
A – B Relative Elements of set A, but not of set B. If set A = {a, b, c} and set B
complement or = {c, d, e}, then
Difference
A – B = {a, b}
A × B Cartesian product The set of ordered pairs (a, b) whereby a is If set A = {1, 2, 3} and B =
an element of A and b is an element of B. {100, 200}, then A × B =

{(1, 100), (2, 100), (3, 100),
(1, 200), (2, 200), (3, 200)}
a ∈ A Element of Membership of set A. If set A = {a, b, e, f, g, h},
then a ∈ A.

a ∉ A Not an element Not a member of set A. If set A = {a, b, e, f, g, h},
of then x ∉ A.

∅ Null or Empty Set The set does not contain any elements. If set A = { }, then A = ∅.

n(A) Number of The number of elements that are in a set. If set A = {a, b, e, f, g, h},
elements then n(A) = 6.

ℕ Set of natural ℕ = {0, 1, 2, 3, 4, 5, 6, 7, 8, ...} 0 ∈ ℕ
numbers

ℤ Set of integers ℤ = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...} -2 ∈ ℤ

ℚ Set of rational A rational number is a number that can be 2
∈ ℚ
numbers expressed as a fraction where p and q are 3
integers and q does not equal zero.

ℝ Set of real The set of all numbers. √2 ∈ ℝ
numbers

48 091math-wb-w3-(sets)