Page 285 - J. C. Turner "History and Science of Knots"

276 History and Science of Knots

relate to and remember.
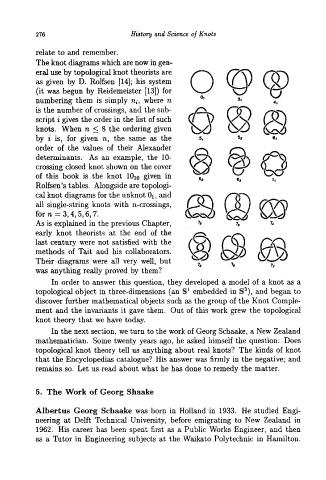
The knot diagrams which are now in gen-
(it was begun by Reidemeister [13]) for o ^
eral use by topological knot theorists are
as given by D. Rolfsen [14]; his system

numbering them is simply nZ, where n
is the number of crossings, and the sub-
script i gives the order in the list of such
knots. When n < 8 the ordering given
by i is, for given n, the same as the 5, 52 61
order of the values of their Alexander
determinants. As an example, the 10- Q D
crossing closed knot shown on the cover
of this book is the knot 1020 given in
6p g8 71
Rolfsen's tables. Alongside are topologi-
cal knot diagrams for the unknot 01, and
all single-string knots with n-crossings,
for n = 3,4,5,6,7.
As is explained in the previous Chapter, 72 78 7,
early knot theorists at the end of the
last century were not satisfied with the
methods of Tait and his collaborators.
Their diagrams were all very well, but
7Q 7e 77
was anything really proved by them?
In order to answer this question, they developed a model of a knot as a
topological object in three-dimensions (an S' embedded in S3), and began to
discover further mathematical objects such as the group of the Knot Comple-
ment and the invariants it gave them. Out of this work grew the topological
knot theory that we have today.
In the next section, we turn to the work of Georg Schaake, a New Zealand
mathematician. Some twenty years ago, he asked himself the question: Does
topological knot theory tell us anything about real knots? The kinds of knot
that the Encyclopedias catalogue? His answer was firmly in the negative; and
remains so. Let us read about what he has done to remedy the matter.

5. The Work of Georg Shaake

Albertus Georg Schaake was born in Holland in 1933. He studied Engi-
neering at Delft Technical University, before emigrating to New Zealand in
1962. His career has been spent first as a Public Works Engineer, and then
as a Tutor in Engineering subjects at the Waikato Polytechnic in Hamilton.