Page 156 - NUMINO TG_6A
P. 156
10Fill It with Chocolate Pieces Unit
tMa erial Rectangular Papers [A2], Ruler, Tape
Math VoCabulary hundreds: numbers from 100 to 999
Objective: Learn how to find the surface areas and volumes of cylinders. Have students keep the same partner. Have
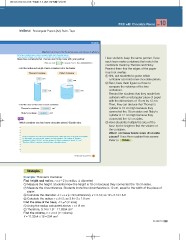
First, have students guess whose container holds more chocolate pieces.
Then have them figure out a method to calculate and compare the volumes.
Make two containers that Thomas and Ricky made with your partner.
What you need: Rectangular Papers (A2), Ruler each team make containers that match the
containers made by Thomas and Ricky.
Find the radius and height of each container. Fill in the blanks. Remind them that the edges of the paper
Thomas’s Container Ricky’s Container must not overlap.
first, ask students to guess which
1.9 cm 2.9 cm container can hold more chocolate pieces.
Next, have them figure out how to
compare the volumes of the two
18 cm 12 cm containers.
Remind the students that they made their
cylinders with a rectangular piece of paper
with the dimensions of 18 cm by 12 cm.
Find the area of the base of each container. Then, they can deduce that Thomas’s
Thomas’s container: 11.3354 cm2
Ricky’s container: 26.4074 cm2 cylinder is 18 cm high because they
Chat connected the 18 cm sides and Ricky’s
Which container can hold more chocolate pieces? Explain why.
cylinder is 12 cm high because they
connected the 12 cm sides.
Have students multiply the area of the
base by the height to find the volume of
the container.
Which container holds more chocolate
Ricky’s container can hold more chocolate pieces. When the area of the base is multiplied pieces? Have them explain their answer.
by the height, you can get the volume of each container. The volume of Thomas’ Refer to .
container is about 204 cm3, and the volume of Ricky’s container is about 317 cm3.
Therefore, Ricky’s container can hold more chocolate pieces.
10. Fill It with Chocolate Pieces 83
Example: Thomas’s Container
Find height and radius, r d 2 (r: radius, d: diameter)
Measure the height. Students know the height is 18 cm because they connected the 18 cm sides.
Measure the circumference. Students know the circumference is 12 cm, equal to the width of the piece of
paper.
Calculate the diameter: d c (c: circumference); 3.14; so 12 3.14 3.8
Calculate the radius: r d 2; so 3.8 2 1.9 cm
Find the area of the base, A r2 (A: area)
Using the radius calculated above, r 1.9 cm
Therefore, 3.14 1.92 11.3354 cm2
Find the volume, V A h (V: volume)
V 11.3354 18 204 cm3
6A Unit 10 139
tMa erial Rectangular Papers [A2], Ruler, Tape
Math VoCabulary hundreds: numbers from 100 to 999
Objective: Learn how to find the surface areas and volumes of cylinders. Have students keep the same partner. Have
First, have students guess whose container holds more chocolate pieces.
Then have them figure out a method to calculate and compare the volumes.
Make two containers that Thomas and Ricky made with your partner.
What you need: Rectangular Papers (A2), Ruler each team make containers that match the
containers made by Thomas and Ricky.
Find the radius and height of each container. Fill in the blanks. Remind them that the edges of the paper
Thomas’s Container Ricky’s Container must not overlap.
first, ask students to guess which
1.9 cm 2.9 cm container can hold more chocolate pieces.
Next, have them figure out how to
compare the volumes of the two
18 cm 12 cm containers.
Remind the students that they made their
cylinders with a rectangular piece of paper
with the dimensions of 18 cm by 12 cm.
Find the area of the base of each container. Then, they can deduce that Thomas’s
Thomas’s container: 11.3354 cm2
Ricky’s container: 26.4074 cm2 cylinder is 18 cm high because they
Chat connected the 18 cm sides and Ricky’s
Which container can hold more chocolate pieces? Explain why.
cylinder is 12 cm high because they
connected the 12 cm sides.
Have students multiply the area of the
base by the height to find the volume of
the container.
Which container holds more chocolate
Ricky’s container can hold more chocolate pieces. When the area of the base is multiplied pieces? Have them explain their answer.
by the height, you can get the volume of each container. The volume of Thomas’ Refer to .
container is about 204 cm3, and the volume of Ricky’s container is about 317 cm3.
Therefore, Ricky’s container can hold more chocolate pieces.
10. Fill It with Chocolate Pieces 83
Example: Thomas’s Container
Find height and radius, r d 2 (r: radius, d: diameter)
Measure the height. Students know the height is 18 cm because they connected the 18 cm sides.
Measure the circumference. Students know the circumference is 12 cm, equal to the width of the piece of
paper.
Calculate the diameter: d c (c: circumference); 3.14; so 12 3.14 3.8
Calculate the radius: r d 2; so 3.8 2 1.9 cm
Find the area of the base, A r2 (A: area)
Using the radius calculated above, r 1.9 cm
Therefore, 3.14 1.92 11.3354 cm2
Find the volume, V A h (V: volume)
V 11.3354 18 204 cm3
6A Unit 10 139