Page 164 - NUMINO TG_6A
P. 164
Challenge Volumes of Containers Unit
jOb ective Find the volume of two containers.
Challenge Volumes of Containers 1. Textbook Instructions
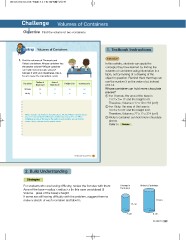
1 . Find the volumes of Thomas’s and In this activity, students can apply the
Ricky’s containers. Whose container has concepts they have learned by finding the
the greater volume? Whose container
can hold more chocolate pieces? volumes of containers using information in a
Discuss it with your classmates. Use 3
for π to make the calculation easier. table, not by looking at a drawing of the
object in question. Remind them that they can
Container Radius of Area of Height (cm) Volume (cm3) use the number 3 as the value of pi, instead
Base (cm) Base (cm2)
Thomas 18 216 of 3.14.
Ricky 2 12 12 324
3 Whose container can hold more chocolate
27
pieces?
For Thomas, the area of the base is
2 2 3 12 and the height is18.
Therefore, Volume 12 18 216 (cm3)
For Ricky, the area of the base is
3 3 3 27 and the height is12.
Ricky’s container can hold more chocolate pieces. The lid of Ricky’s container has an Therefore, Volume 27 12 324 (cm3)
area of 27 cm2, and the lid of Thomas’s container has an area of 12 cm2. When
Ricky’s container can hold more chocolate
multiplying the area of the base by the height of each container, you can find the
pieces.
volume. Ricky’s container has the greater volume.
Refer to .
10. Fill It with Chocolate Pieces 91
2. Build Understanding
For students who are having difficulty, review the fomulas with them: Thomas’s Ricky’s Container
Area of the base radius radius (in this case considered 3) Container
Volume (area of the base) height
If some are still having difficulty with the problem, suggest them to 18 cm
make a sketch of each container and label it.
3 cm
12 cm 6A Unit 10 147
2 cm
jOb ective Find the volume of two containers.
Challenge Volumes of Containers 1. Textbook Instructions
1 . Find the volumes of Thomas’s and In this activity, students can apply the
Ricky’s containers. Whose container has concepts they have learned by finding the
the greater volume? Whose container
can hold more chocolate pieces? volumes of containers using information in a
Discuss it with your classmates. Use 3
for π to make the calculation easier. table, not by looking at a drawing of the
object in question. Remind them that they can
Container Radius of Area of Height (cm) Volume (cm3) use the number 3 as the value of pi, instead
Base (cm) Base (cm2)
Thomas 18 216 of 3.14.
Ricky 2 12 12 324
3 Whose container can hold more chocolate
27
pieces?
For Thomas, the area of the base is
2 2 3 12 and the height is18.
Therefore, Volume 12 18 216 (cm3)
For Ricky, the area of the base is
3 3 3 27 and the height is12.
Ricky’s container can hold more chocolate pieces. The lid of Ricky’s container has an Therefore, Volume 27 12 324 (cm3)
area of 27 cm2, and the lid of Thomas’s container has an area of 12 cm2. When
Ricky’s container can hold more chocolate
multiplying the area of the base by the height of each container, you can find the
pieces.
volume. Ricky’s container has the greater volume.
Refer to .
10. Fill It with Chocolate Pieces 91
2. Build Understanding
For students who are having difficulty, review the fomulas with them: Thomas’s Ricky’s Container
Area of the base radius radius (in this case considered 3) Container
Volume (area of the base) height
If some are still having difficulty with the problem, suggest them to 18 cm
make a sketch of each container and label it.
3 cm
12 cm 6A Unit 10 147
2 cm