Page 41 - NUMINO TG_6A
P. 41
Activity 3 Numbers, Their GCF and LCM
jOb ective Learn the relationship between greatest common factor and least common multiple.
1. Textbook Instructions Activity 3 Numbers, Their GCF and LCM
This activity calls on students to observe and Have students fill out the table by finding the products of the numbers,
interpret the relationship between the greatest
common factor and least common multiple of 1 the GCF, and the LCM. Then have them find the product of GCF and the LCM.
two numbers.
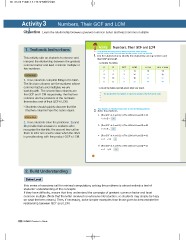
. Use the tables below to identify the relationship among numbers and
1. Have students complete filling in the table. their GCF and LCM.
The first two columns are the numbers whose
common factors and multiples we are Complete the tables.
working with. The second two columns are
the GCF and LCM respectively; the final two AB GCF LCM AB GCF LCM
columns are the products of the numbers 27 1 14 14 14
themselves and of their GCF LCM. 35 1 15 15
5 10 10 15
Students should quickly discover that the 68 5 50 50
final two columns have the same values. 24 48
2 48
2. Have students solve the problems. 2a and
2b provide their answers to students who Look at the tables and talk about what you found.
recognize the identity; the second two call on
them to infer one source value when the other The product of the two numbers is equal to the product of the GCF and the LCM.
is provide along with the product GCF LCM.
2 Have students use what they found above to solve the following problems.
. Solve the problems.
a. (The GCF of A and B) (The LCM of A and B) = 24
A B = 24
b. (The GCF of A and B) (The LCM of A and B) = 40
A B = 40
c. (The GCF of A and B) (The LCM of A and B) = 42
A = 7, B = 6
d. (The GCF of A and B) (The LCM of A and B) = 56
A = 4, B = 14
16
2. Build Understanding
This series of exercises call for minimal computation; solving the problems is almost entirely a test of
students’ understanding of the concepts.
If they have difficulty, ensure that they understand the concepts of greatest common factor and least
common multiple. (Note that the latter received no extensive introduction, so students may simply be hazy
on what the term means.) Then, if necessary, solve simpler examples than those given to demonstrate the
relationship between GCF and LCM.
024 NUMINO Teacher s Guide
jOb ective Learn the relationship between greatest common factor and least common multiple.
1. Textbook Instructions Activity 3 Numbers, Their GCF and LCM
This activity calls on students to observe and Have students fill out the table by finding the products of the numbers,
interpret the relationship between the greatest
common factor and least common multiple of 1 the GCF, and the LCM. Then have them find the product of GCF and the LCM.
two numbers.
. Use the tables below to identify the relationship among numbers and
1. Have students complete filling in the table. their GCF and LCM.
The first two columns are the numbers whose
common factors and multiples we are Complete the tables.
working with. The second two columns are
the GCF and LCM respectively; the final two AB GCF LCM AB GCF LCM
columns are the products of the numbers 27 1 14 14 14
themselves and of their GCF LCM. 35 1 15 15
5 10 10 15
Students should quickly discover that the 68 5 50 50
final two columns have the same values. 24 48
2 48
2. Have students solve the problems. 2a and
2b provide their answers to students who Look at the tables and talk about what you found.
recognize the identity; the second two call on
them to infer one source value when the other The product of the two numbers is equal to the product of the GCF and the LCM.
is provide along with the product GCF LCM.
2 Have students use what they found above to solve the following problems.
. Solve the problems.
a. (The GCF of A and B) (The LCM of A and B) = 24
A B = 24
b. (The GCF of A and B) (The LCM of A and B) = 40
A B = 40
c. (The GCF of A and B) (The LCM of A and B) = 42
A = 7, B = 6
d. (The GCF of A and B) (The LCM of A and B) = 56
A = 4, B = 14
16
2. Build Understanding
This series of exercises call for minimal computation; solving the problems is almost entirely a test of
students’ understanding of the concepts.
If they have difficulty, ensure that they understand the concepts of greatest common factor and least
common multiple. (Note that the latter received no extensive introduction, so students may simply be hazy
on what the term means.) Then, if necessary, solve simpler examples than those given to demonstrate the
relationship between GCF and LCM.
024 NUMINO Teacher s Guide