Page 154 - NUMINO Challenge_B2

Problem solving 2 CD

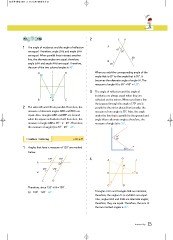
1 The angle of incidence and the angle of reflection A
65
are equal. Therefore, angle DHE and angle EHA 55
are equal. When parallel lines intersect another
line, the alternate angles are equal; therefore, B
angle EAH and angle AHB are equal. Therefore, 65
the sum of the two colored angles is 90°.
When you add the corresponding angle of the
AED angle that is 65° to the angle that is 55°, it
becomes the alternate angle of angle . The
B HC measure of angle is 65 55 120 .

2 The sides AB and CD are parallel. Therefore, the 3 The angle of reflection and the angle of

measure of alternate angles ABD and BDC are incidence are always equal when they are
equal. Also, triangles ABE and BEF are formed reflected on the mirror. When you draw a line
when the square is divided in half; therefore, the that passes through the angle of 70° and is
measure of angle ABE is 90 2 45 . Therefore, parallel to the mirror placed horizontally, the
the measure of angle is 72 45 27 . measure of one angle is 35°. Also, the angle
under the line that is parallel to the ground and
angle are alternate angles; therefore, the
measure of angle is 35°.

Creative Thinking p.66~p.67 35
35
1 Angles that have a measure of 120° are marked
4 AG F
below.
H
120 120 BE
A
CD
120 120 Triangles ACG and triangle AEB are identical;
B therefore, the angles ACG and BEA are equal.
Also, angles HEF and DHE are alternate angles;
CD 180 , therefore, they are equal. Therefore, the sum of
the two marked angles is 90°.
Therefore, since 120
180 120 60 .

Answer Key