Page 38 - Cálculo Integral: Guía I

INSTITUTO POLITÉCNICO NACIONAL
CECYT “WILFRIDO MASSIEU”
Unidades de Aprendizaje del Área Básica

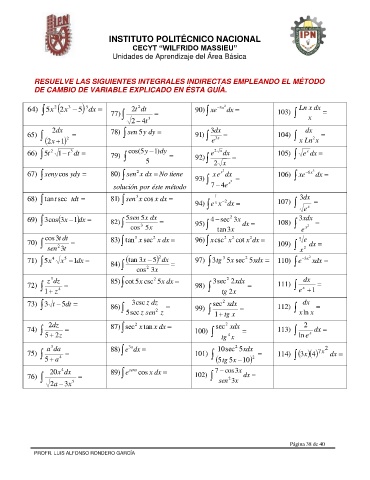
RESUELVE LAS SIGUIENTES INTEGRALES INDIRECTAS EMPLEANDO EL MÉTODO
DE CAMBIO DE VARIABLE EXPLICADO EN ÉSTA GUÍA.


5
64)  5 x 2  x2 3 5  dx 77 )  2 dtt 2  90 )  xe  x3 2 dx  103)  Ln x dx 
2  4t 3 x
65)  2dx  78 )  sen 5 y dy  91 )  3 dx  104)  dx 
2x 1  2 e 3 x x Ln 2 x

2
66)  t 5 2 1  dtt 3  79 )  cos( 5y 5  )1 dy  92 )  e 2 x dx  105)  e x dx 
x
67)  senycos ydy  80 )  sen 2 x dx  No tiene 93 )  x e x 2 dx  106)  xe  x6 2 dx 

solución por éste método 7  4e x 2
68)  tan tsec tdt  81 )  sen 3 x cos x dx  94 )  e 1 x x 2 dx  107)  3 dx x 
e

69)  3 cos  x3 1 dx 82 )  5 sen 5 x x dx  95 )  4 sec 2 x 3 x 3 dx  108)  3xdx 
3
2
cos
5
tan
e
x
2
70)  cos 2 t 3 dt  83 )  tan 3 x sec 2 x dx  96 )  xcsc 2 x cot x 2 dx  109)  x x e dx 
sen
t 3
2
2
3
x 3
71)  5 x 4 x 5  dx1  84 )  tan cos 2 5 x 3  dx  97)  3 tg 5 x sec 2 5 xdx  110)  e  x3 2 xdx 
3
dz
72)  1 z  z 4  85 )  cot 5 x csc 2 x 5 dx  98)  3 sec 2 2 x 2 xdx  111)  e x dx 
1
tg
dx
dz
z
3
csc
73)  3 t  dt5  86 )  5 sec z sen 2 z  99)  sec 2 xdx  112)  xln x 
 tg
1
x
dz
74)  5 2  z2  87 )  sec 2 xtan x dx  100)  sec 2 4 xdx  113)  ln 2 e x dx 
x
tg
3
da
5xdx
10
75)  5 a  a 4  88 )  e 3 x dx  101)  5tg sec 2 10  2  114)     43 x 7 x 2 dx 
5x
76)  20 dxx 4  89 )  e senx cos x dx  102)  7  cos x 3 dx 
2
2a  3x 5 sen x 3

Página 38 de 40
PROFR. LUIS ALFONSO RONDERO GARCÍA