Page 79 - Secundaria - Matemáticas 3 - McGraw Hill

b) ¿Qué relación encuentran entre el número de lados y el número de diagonales de cada polígono de la tabla? ______________________________________________________________________
c) ¿Cuántas diagonales tiene un polígono de 12 lados? _______ ¿Cómo lo determinarían? ______________________________________________________________________
d) La expresión algebraica que relaciona el número de lados y el de las diagonales es: N 5 n(n 2 3). Analicen con sus compañeros a qué se refiere la variable “N”
y a qué, la variable “n”.
e) ¿Cuántos lados tiene un polígono de 27 diagonales? ___________ ¿Y uno de 90 diagonales?
______________________________________________________________________
f) Analicen con sus compañeros las respuestas obtenidas, comparen las estrategias que siguieron para contestar las preguntas y escriban en su cuaderno las ideas principales.
Actividad 2. Entre gráficas y raíces
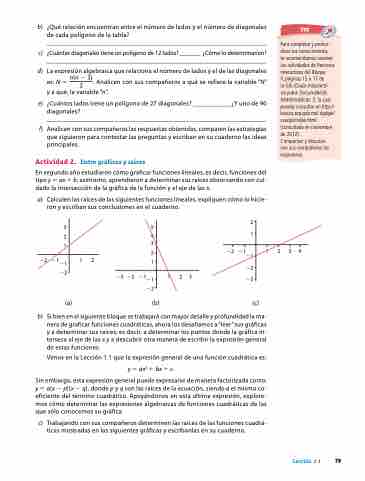
En segundo año estudiaron cómo graficar funciones lineales, es decir, funciones del tipo y 5 ax 1 b; asimismo, aprendieron a determinar sus raíces observando con cui- dado la intersección de la gráfica de la función y el eje de las x.
a) Calculen las raíces de las siguientes funciones lineales, expliquen cómo lo hicie- ron y escriban sus conclusiones en el cuaderno.
TIC
Para completar y profun- dizar tus conocimientos,
te recomendamos resolver las actividades de Recursos interactivos del Bloque
II, páginas 15 a 17 de
la GIS (Guía interacti- va para Secundaria): Matemáticas 3, la cual puedes consultar en http:// basica.sep.gob.mx/ dgdgie/ cva/gis/index.html: (consultada en noviembre de 2012) .
Compartan y discutan
con sus compañeros las respuestas.
2
35 24
2 1
1 222121 1 2
22
(a)
3 2 1
23222121 22
(b)
2221 1234 21
22 123 23
(c)
b) Si bien en el siguiente bloque se trabajará con mayor detalle y profundidad la ma- nera de graficar funciones cuadráticas, ahora los desafiamos a “leer” sus gráficas y a determinar sus raíces; es decir, a determinar los puntos donde la gráfica in- terseca al eje de las x y a descubrir otra manera de escribir la expresión general de estas funciones.
Vimos en la Lección 1.1 que la expresión general de una función cuadrática es: y 5 ax2 1 bx 1 c.
Sin embargo, esta expresión general puede expresarse de manera factorizada como: y 5 a(x 2 p)(x 2 q), donde p y q son las raíces de la ecuación, siendo a el mismo co- eficiente del término cuadrático. Apoyándonos en esta última expresión, explore- mos cómo determinar las expresiones algebraicas de funciones cuadráticas de las que sólo conocemos su gráfica.
c) Trabajando con sus compañeros determinen las raíces de las funciones cuadrá- ticas mostradas en las siguientes gráficas y escríbanlas en su cuaderno.
Lección 2.1 79