Page 137 - Buku Teks Digital Mate KSSM T5

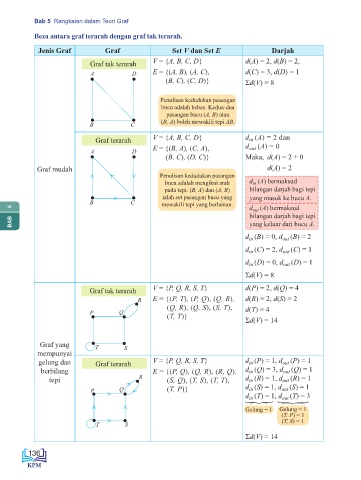
Bab 5 Rangkaian dalam Teori Graf

Beza antara graf terarah dengan graf tak terarah.

Jenis Graf Graf Set V dan Set E Darjah
Graf tak terarah V = {A, B, C, D} d(A) = 2, d(B) = 2,
A D E = {(A, B), (A, C), d(C) = 3, d(D) = 1
(B, C), (C, D)} Σd(V) = 8

Penulisan kedudukan pasangan
bucu adalah bebas. Kedua-dua
pasangan bucu (A, B) atau
(B, A) boleh mewakili tepi AB.
B C

Graf terarah V = {A, B, C, D} d (A) = 2 dan
in
A D E = {(B, A), (C, A), d out (A) = 0
(B, C), (D, C)} Maka, d(A) = 2 + 0
Graf mudah d(A) = 2
> > > Penulisan kedudukan pasangan
bucu adalah mengikut arah d (A) bermaksud
in
pada tepi. (B, A) dan (A, B) bilangan darjah bagi tepi
> ialah set pasangan bucu yang yang masuk ke bucu A.
B C mewakili tepi yang berlainan.
5 d out (A) bermaksud
BAB bilangan darjah bagi tepi
yang keluar dari bucu A.

d (B) = 0, d out (B) = 2
in
d (C) = 2, d out (C) = 1
in
d (D) = 0, d out (D) = 1
in
Σd(V) = 8

Graf tak terarah V = {P, Q, R, S, T} d(P) = 2, d(Q) = 4
R E = {(P, T), (P, Q), (Q, R), d(R) = 2, d(S) = 2
(Q, R), (Q, S), (S, T), d(T) = 4
P Q (T, T)} Σd(V) = 14

Graf yang T S
mempunyai
gelung dan Graf terarah V = {P, Q, R, S, T} d (P) = 1, d out (P) = 1
in
berbilang E = {(P, Q), (Q, R), (R, Q), d (Q) = 3, d out (Q) = 1
in
tepi > R (S, Q), (T, S), (T, T), d (R) = 1, d out (R) = 1
in
in
P > Q > (T, P)} d (S) = 1, d out (S) = 1
(T) = 3
d (T) = 1, d
in }
> > Gelung = 1 Gelung = 1
out }
> (T, P) = 1
(T, S) = 1
T S
Saiz sebenar
Σd(V) = 14
136