Page 33 - Buku Paket Kelas 8 Matematika Semester 2
P. 33
CF baba
AcBDxE
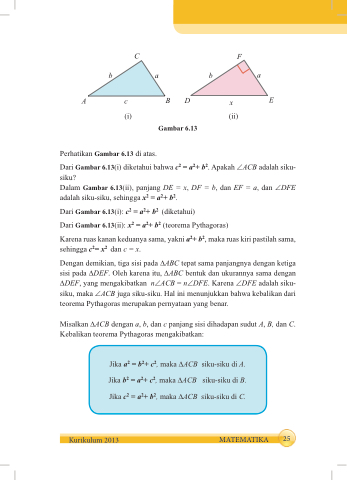
(i) Perhatikan Gambar 6.13 di atas.
(ii)
Gambar 6.13
Dari Gambar 6.13(i) diketahui bahwa c2 = a2+ b2. Apakah ∠ACB adalah siku- siku?
Dalam Gambar 6.13(ii), panjang DE = x, DF = b, dan EF = a, dan ∠DFE adalah siku-siku, sehingga x2 = a2+ b2.
Dari Gambar 6.13(i): c2 = a2+ b2 (diketahui)
Dari Gambar 6.13(ii): x2 = a2+ b2 (teorema Pythagoras)
Karena ruas kanan keduanya sama, yakni a2+ b2, maka ruas kiri pastilah sama, sehingga c2= x2 dan c = x.
Dengan demikian, tiga sisi pada ∆ABC tepat sama panjangnya dengan ketiga sisi pada ∆DEF. Oleh karena itu, ∆ABC bentuk dan ukurannya sama dengan ∆DEF, yang mengakibatkan n∠ACB = n∠DFE. Karena ∠DFE adalah siku- siku, maka ∠ACB juga siku-siku. Hal ini menunjukkan bahwa kebalikan dari teorema Pythagoras merupakan pernyataan yang benar.
Misalkan ∆ACB dengan a, b, dan c panjang sisi dihadapan sudut A, B, dan C. Kebalikan teorema Pythagoras mengakibatkan:
Jika a2 = b2+ c2, maka ∆ACB siku-siku di A. Jika b2 = a2+ c2, maka ∆ACB siku-siku di B. Jika c2 = a2+ b2, maka ∆ACB siku-siku di C.
25
Kurikulum 2013 MATEMATIKA