Page 8 - I

th
STRUCTURAL RELIABILITY AND RISK ANALYSIS – 4 Year FILS

Table 1.1. Sample of 30 values of the compressive strength of concrete, daN/cm2

320 380 340 360 330 360 380 360 320 350
350 340 350 360 370 350 350 420 360 340
370 390 370 370 400 360 400 350 360 390

The statistical relevance of the information contained in Table 1.1 can be revealed if one shall
order the data in ascending order in Table 1.2, first column (320, 330 and so on).

Table 1.2 Frequencies of values of random variable listed in Table 1.1

Compressive Absolute Relative Cumulative Cumulative relative
strength frequency frequency frequency frequency
320 2 0.067 2 0.067
330 1 0.033 3 0.100
340 3 0.100 6 0.200
350 6 0.200 12 0.400
360 7 0.233 19 0.633
370 4 0.133 23 0.767
380 2 0.067 25 0.833
390 2 0.067 27 0.900
400 2 0.067 29 0.967
410 0 0.000 29 0.967
420 1 0.033 30 1.000

The number of occurring figures from Table 1.1 is listed in the second column of Table 1.2. It
indicates how often the corresponding value x occurs in the sample and is called absolute
frequency of that value x in the sample.

Dividing it by the size n of the sample one obtains the relative frequency listed in the third
column of Table 1.2.

If for a certain value x one sums all the absolute frequencies corresponding to the sample
values which are smaller than or equal to that x, one obtains the cumulative frequency
corresponding to that x. This yields the values listed in column 4 of Table 1.2. Division by the
size n of the sample yields the cumulative relative frequency in column 5 of Table 1.2.

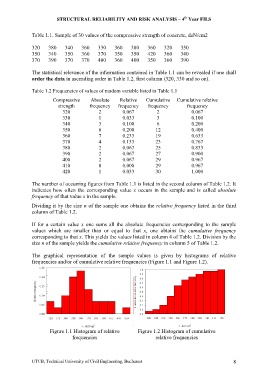
The graphical representation of the sample values is given by histograms of relative
frequencies and/or of cumulative relative frequencies (Figure 1.1 and Figure 1.2).

Figure 1.1 Histogram of relative Figure 1.2 Histogram of cumulative
frequencies relative frequencies

UTCB, Technical University of Civil Engineering, Bucharest 8