Page 305 - chapter 1
P. 305
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης 305
ΠΑΡΑΔΕΙΓΜΑΤΑ
1. ΘΕΩΡΗΜΑ BOLZANO (ΚΛΕΙΣΤΟ ΔΙΑΣΤΗΜΑ)
Δίνεται συνεχής συνάρτηση f : [2, 3] [2, 3] .
Να αποδείξετε οτι υπάρχει ένα τουλάχιστον ξ [2, 3]
6
τέτοιο, ώστε f(ξ)= ξ .
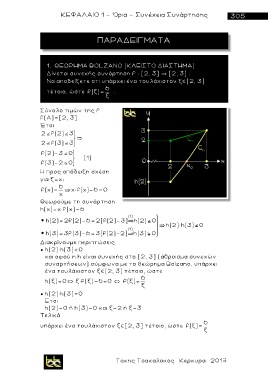
Σύνολο τιμών της f
f(A)=[2, 3]
Έτσι
2 f(2) 3
2 f(3) 3
f(2)-3 0
(1)
f(3)-2 0
Η προς απόδειξη σχέση
για ξ=χ:
6
f(x)= x× f(x)-6 = 0
x
Θεωρούμε τη συνάρτηση
h(x)=χ f(x)-6
h(2)= 2f(2)-6 = 2[f(2)-3] (1) h(2) 0
h(2)× h(3) 0
h(3)= 3f(3)-6 = 3[f(2)-2] (1) h(3) 0
Διακρίνουμε περιπτώσεις
● h(2) h(3)<0
και αφού η h είναι συνεχής στο [2, 3] (άθροισμα συνεχών
συναρτήσεων) σύμφωνα με το θεώρημα Bolzano, υπάρχει
ένα τουλάχιστον ξ (2, 3) τέτοιο, ώστε
6
h(ξ)=0` ξ f( ξ ) -6=0 ` f(ξ)=
ξ
● h(2) h(3)=0
Ετσι
h(2)=0 ή h(3)=0 και ξ=2 ή ξ=3
Τελικά
6
υπάρχει ένα τουλάχιστον ξ [2, 3] τέτοιο, ώστε f(ξ)=
ξ
Τακης Τσακαλακος Κερκυρα 2017