Page 9 - Kelas XI_Matematika Umum_KD 3.8
P. 9
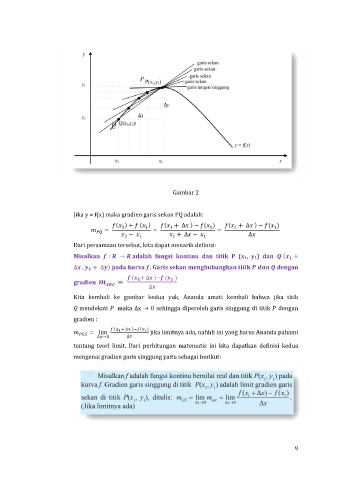
Gambar 2
Jika y = f(x) maka gradien garis sekan PQ adalah:
( ) + ( ) ( + ∆ ) − ( ) ( + ∆ ) − ( )
5
5
2
5
5
5
-. = − 5 = + ∆ − 5 = ∆
5
2
Dari persamaan tersebut, kita dapat menarik definisi:
Misalkan ∶ → adalah fungsi kontinu dan titik P (x1, y1) dan ( +
∆ , + ∆ ) pada kurva . Garis sekan menghubungkan titik dengan
gradien = ( I ∆ )* ( )
∆
Kita kembali ke gambar kedua yuk, Ananda amati kembali bahwa jika titik
mendekati maka ∆x ⇾ 0 sehingga diperoleh garis singgung di titik dengan
gradien :
-LM = lim R (, + I ∆, )*R(, + ) jika limitnya ada, nahhh ini yang harus Ananda pahami
∆,→Q ∆,
tentang teori limit. Dari perhitungan matematis ini kita dapatkan definisi kedua
mengenai gradien garis singgung yaitu sebagai berikut:
9