Page 45 - Echte wiskunde
P. 45
Echte Wiskunde
33
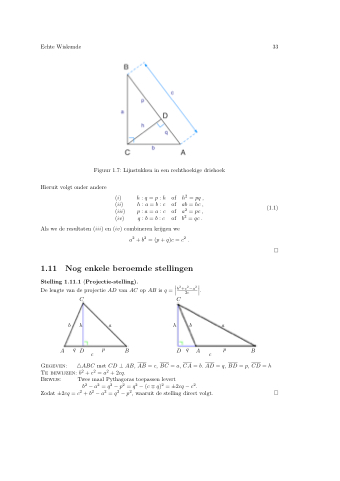
Figuur 1.7: Lijnstukken in een rechthoekige driehoek Hieruit volgt onder andere
(i) h:q=p:h of h2 =pq,
(ii) h:a=b:c of ab=hc,
(iii) p:a=a:c of a2 =pc,
(iv) q : b = b : c of b2 = qc .
Als we de resultaten (iii) en (iv) combineren krijgen we
a2 +b2 =(p+q)c=c2 .
1.11 Nog enkele beroemde stellingen
Stelling 1.11.1 (Projectie-stelling). b2+c2−a2 De lengte van de projectie AD van AC op AB is q = 2c .
CC
bhahba
AqDcpB DqAcpB
(1.1)
Gegeven: △ABC met CD ⊥ AB, AB = c, BC = a, CA = b. AD = q, BD = p, CD = h Te bewijzen: b2 + c2 = a2 + 2cq.
Bewijs: Twee maal Pythagoras toepassen levert
b2 −a2 =q2 −p2 =q2 −(c∓q)2 =±2cq−c2. Zodat ±2cq = c2 + b2 − a2 = q2 − p2, waaruit de stelling direct volgt.