Page 47 - Math SL HB Sem 2

Area between Curves

The use of the definite integral in finding the area ofa region enclosed by a single curve can be
extended to finding the area enclosed between two curves. Although we do have a compact
formula to hnd such areas, in reality it is a simple geometrical observation.

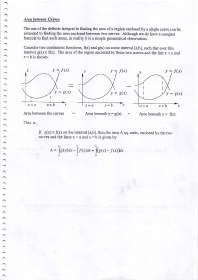
Consider two continuous fiurctions, (x) and g(x) on some interval [a,b], such that over this
interval g(x) > (x). The area of the region enclosed by these two curyes and the line x : a and
x:bisshown.

v v f (x) v v f(x) v v f (x)

v = B(x) v = 8(r) v=8G)

x=a r=b x x=a x=b x -r=a x=b x

Area between the curves Areabeneathy:g(x) Area beneath y: f(x)

That is ,

If g(x) > f(x) on the interval [a,b], then the area A sq. units, enclosed by the rwo
curves and the lines x : a and x : b is given by

bbb
A:
[s?)dx- lt7v,- lG@- f <,>)a,