Page 14 - Decimale_5_Theme_6+revision_2017-08-23

secTIon 6.5 GéoMétriE Expérimenter la relation d’Euler sur des polyèdres convexes

J’apprends

Expérimenter la relation d’Euler sur des polyèdres convexes

e
Au 18 siècle, le grand mathématicien Leonhard Euler a découvert
une formule qui permet de calculer facilement la relation entre le
nombre de faces (F), de sommets (S) et d’arêtes (a) d’un polyèdre
convexe. On nomme cette formule « relation d’Euler ».

La relation d’Euler : F + S – 2 = a

• On additionne le nombre de faces et de sommets.

• On soustrait 2 de ce nombre.
• Le résultat qu’on obtient est le nombre d’arêtes.

Exemple :

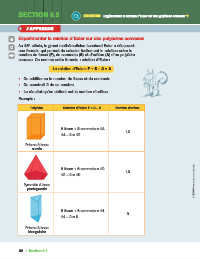
Polyèdre Relation d’Euler : F + S – 2 Nombre d’arêtes

6 faces + 8 sommets = 14
12
14 – 2 = 12

Prisme à base
carrée

6 faces + 6 sommets = 12
10
12 – 2 = 10

Pyramide à base
pentagonale

5 faces + 6 sommets = 11
9
11 – 2 = 9

Prisme à base
triangulaire

92 Section 6.5

13229_decimale_5b_th06.indd 92 25/03/13 12:16 PM