Page 15 - modul trigonometri_Neat
P. 15
Example 1.2
1
Given the right triangle ABC, sin A = . Specify cos A and tan A
3
Alternative Solutions
1 1
Known sin A = , that is = . More precisely, the side length (BC) in
3 3
front of angle A and the length of the sloped side (AC) of the ABC
triangle have a ratio of 1 : 3,
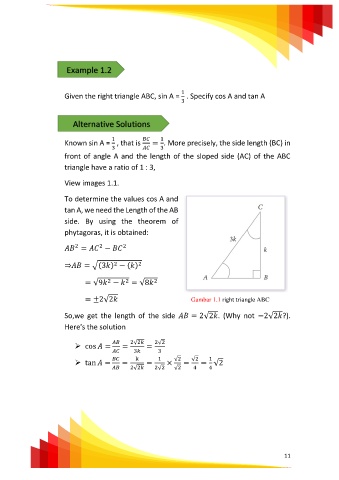
View images 1.1.
To determine the values cos A and
tan A, we need the Length of the AB
side. By using the theorem of
phytagoras, it is obtained:
2
2
2
= −
2
2
⇒ = √(3 ) − ( )
2
2
2
= √9 − = √8
= ±2√2 Gambar 1.1 right triangle ABC
So,we get the length of the side = 2√2 . (Why not −2√2 ?).
Here's the solution
2√2 2√2
cos = = =
3 3
k 1 √2 √2 1
tan = = = × = = √2
2√2 2√2 √2 4 4
11