Page 4 - The $ game .dvi

144 The European Physical Journal B

1
Price p(t) 10 0 0.9 . T=100

0.8
0 50 100 150 200 Time t 300 350 400 450 500 0.7 o T=200
250
Wealth of Market−maker W(t) 10 0 P(m) 0.6 x T=400
0.5
+ T=800

200
100
150
250
0
50
Time t 300 350 400 450 500 0.4 * T=1600
0.2 0.3 square T=3200
Return −0.2 0 0.2 diamond T=6400
0.1
−0.4
1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 1.2 0
Risk 0 2 4 6 8 10 12
m
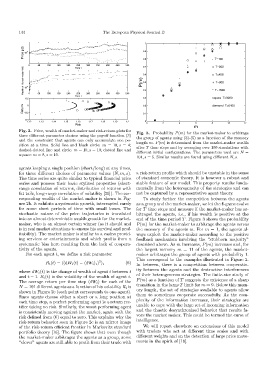
Fig. 2. Price, wealth of market-maker and risk-return plots for
Fig. 3. Probability P(m) for the market-maker to arbitrage
three different parameter choices using the payoff function (3) the group of agents using (3)-(5) as a function of the memory
and the constraint that agents can only accumulate one po- length m. P(m) is determined from the market-maker wealth
sition at a time. Solid line and black circle: m =10,s =4;
after T time steps and by averaging over 100 simulations with
dashed-dotted line and circle: m =10,s = 10; dotted line and different initial configurations. The parameters used are N =
square: m =8,s = 10.
101,s = 5. Similar results are found using different N, s.
agents keeping a single position (short/long) at any times,
for three different choices of parameter values (N, m, s). a risk-return profile which should be unstable in the sense
The time series are quite similar to typical financial price of standard economic theory. It is however a robust and
series and possess their basic stylized properties (short- stable feature of our model. This property results funda-
range correlation of returns, distribution of returns with mentally from the heterogeneity of the strategies and can
fat tails, long-range correlation of volatility [20]). The cor- not be captured by a representative agent theory.
responding wealth of the market maker is shown in Fig- To study further the competition between the agents
ure 2b. It exhibits a systematic growth, interrupted rarely as a group and the market-maker, we let the $-game evolve
for some short periods of time with small losses. The for T time steps and measure if the market-maker has ar-
stochastic nature of the price trajectories is translated bitraged the agents, i.e., if his wealth is positive at the
into an almost deterministic wealth growth for the market- end of the time period T . Figure 3 shows the probability
maker, who is an almost certain winner (as it should and
P(m) for the market-maker to arbitrage the agents versus
is in real market situations to ensure his survival and prof- the memory of the agents m.For m = 1, the agents al-
itability). The market maker is similar to a casino provid- ways exploit the market-maker according to the positive
ing services or entertainments and which profits from a feedback mechanism involving the “stubborn majority”
systematic bias here resulting from the lack of coopera- described above. As m increases, P(m) increases and, for
tivity of the agents. the largest memory m = 11 of the agents, the market-
For each agent i, we define a risk parameter maker arbitrages the group of agents with probability 1.
This correspond to the examples illustrated in Figure 2.
2
In between, there is a competition between cooperativ-
R i (t)= (dW i (t) −dW i t ) t (6)
ity between the agents and the destructive interferences
where dW i (t) is the change of wealth of agent i between t of their heterogeneous strategies. The finite-size study of
and t − 1. R i (t) is the volatility of the wealth of agent i.
The average return per time step dW i for each of the P(m) as a function of T suggests the existence of a sharp
N = 101 different agents as a function of his volatility R i is transition in the large T limit for m ≈ 9. Below this mem-
ory length, the set of strategies available to agents allow
shown in Figure 2c (each point corresponds to one agent).
Since agents choose either a short or a long position at them to sometimes cooperate successfully. As the com-
each time step, a perfect performing agent is a return rec- plexity of the information increases, their strategies are
tifier taking no risk. Similarly, the worst performing agent unable to cope with the large set of incoming information
is consistently moving against the market, again with the and the chaotic desynchronized behavior that results fa-
risk defined from (6) equal to zero. This explains why the vors the market maker. This could be termed the curse of
intelligence.
risk-return behavior seen in Figure 2c is an mirror image
of the risk-return efficient frontier in Markovitz standard We will report elsewhere on extensions of this model
portfolio theory [16]. The figure shows that even though with traders who act at different time scales and with
the market-maker arbitrages the agents as a group, some different weights and on the detection of large price move-
“clever” agents are still able to profit from their trade with ments in the spirit of [18].