Page 189 - Matematica 1° Sec
P. 189
Capítulo 21
Geometría analítica III
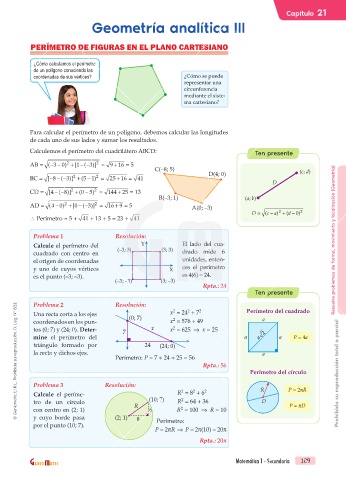
PERÍMETRO DE FIGURAS EN EL PLANO CARTESIANO
¿Cómo calculamos el perímetro
de un polígono conociendo las
coordenadas de sus vértices? ¿Cómo se puede
representar una
circunferencia
mediante el siste-
ma cartesiano?
Para calcular el perímetro de un polígono, debemos calcular las longitudes
de cada uno de sus lados y sumar los resultados.
Calculemos el perímetro del cuadrilátero ABCD: Ten presente
+
2
2
AB = (−−30 ) + [ − (−3 )] = 916 = 5
1
C(–8; 5) (c; d)
2
2
+
BC = [−−8 (−3 )] + ( −51 ) = 25 16 = 41 D(4; 0)
D
2
2
CD = [4 −− )] + (05 ) = 144 25 = 13
+
−
( 8
B(–3; 1) (a; b)
2
2
AD = (40− ) + [0 −− )] = 16 9 = 5 A(0; –3)
+
( 3
D = (c – a) (d – b)
Perímetro = 5 + 41 + 13 + 5 = 23 + 41
Problema 1 Resolución: Resuelve problemas de forma, movimiento y localización (Geometría)
Calcule el perímetro del Y El lado del cua-
cuadrado con centro en (–3; 3) (3; 3) drado mide 6
el origen de coordenadas unidades, enton-
y uno de cuyos vértices X ces el perímetro
es el punto (–3; –3). es 4(6) = 24.
(–3; –3) (3; –3)
Rpta.: 24
Ten presente
Problema 2 Resolución:
Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
2
2
Una recta corta a los ejes x = 24 + 7 2 Perímetro del cuadrado
(0; 7)
2
coordenados en los pun- x = 576 + 49 a
x
2
tos (0; 7) y (24; 0). Deter- x = 625 x = 25 2
7
mine el perímetro del a a a P = 4a
triángulo formado por 24 (24; 0)
la recta y dichos ejes. a
Perímetro: P = 7 + 24 + 25 = 56
Rpta.: 56
Perímetro del círculo Prohibida su reproducción total o parcial
Problema 3 Resolución: R P = 2pR
2
2
Calcule el períme- R = 8 + 6 2
(10; 7)
2
tro de un círculo R = 64 + 36 D P = pD
R
2
6
con centro en (2; 1) R = 100 R = 10
y cuyo borde pasa Perímetro:
(2; 1)
8
por el punto (10; 7).
P = 2pR P = 2p(10) = 20p
Rpta.: 20p
Matemática 1 - Secundaria 189