Page 255 - Matematica 1° Sec
P. 255
Capítulo 23
Razones trigonométricas de
ángulos de cualquier medida I
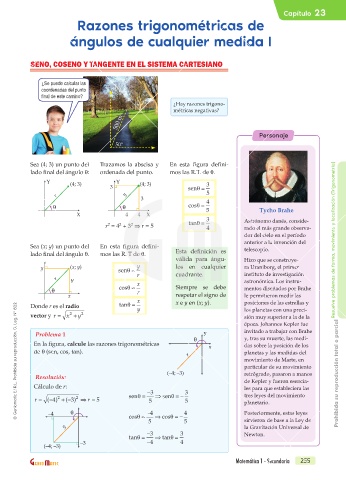
SENO, COSENO Y TANGENTE EN EL SISTEMA CARTESIANO
¿Se puede calcular las
coordenadas del punto
final de este camino?
¿Hay razones trigono-
métricas negativas?
500 m
Personaje
50°
Sea (4; 3) un punto del Trazamos la abscisa y En esta figura defini-
lado final del ángulo q: ordenada del punto. mos las R.T. de q.
Y (4; 3) 3 Y (4; 3) senθ= 3
r 5 5
3 4
cosθ=
5 Tycho Brahe
X 4 4 X 3
2
2
2
r = 4 + 3 r = 5 tanθ= 4 Astrónomo danés, conside-
rado el más grande observa-
dor del cielo en el período
anterior a la invención del Resuelve problemas de forma, movimiento y localización (Trigonometría)
Sea (x; y) un punto del En esta figura defini- telescopio.
lado final del ángulo q. mos las R. T de q. Esta definición es
válida para ángu- Hizo que se construye-
y (x; y) senθ= y los en cualquier ra Uraniborg, el primer
r cuadrante. instituto de investigación
r y astronómica. Los instru-
cosθ= x Siempre se debe mentos diseñados por Brahe
x r respetar el signo de le permitieron medir las
Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
Donde r es el radio tanθ= x x e y en (x; y). posiciones de las estrellas y
y
los planetas con una preci-
2
vector y r = x + y 2 sión muy superior a la de la
época. Johannes Kepler fue
Problema 1 y invitado a trabajar con Brahe
y, tras su muerte, las medi-
En la figura, calcule las razones trigonométricas x das sobre la posición de los
de q (sen, cos, tan). planetas y las medidas del
r
movimiento de Marte, en
particular de su movimiento
(–4; –3) retrógrado, pasaron a manos Prohibida su reproducción total o parcial
Resolución:
de Kepler y fueron esencia-
Cálculo de r: −3 3 les para que estableciera las
4
r
r = ( − ) 2 +− ) 2 ⇒= 5 senθ = 5 ⇒ senθ = − 5 tres leyes del movimiento
3
(
planetario.
–4 cosθ = −4 ⇒ cosθ = − 4 Posteriormente, estas leyes
5 5 sirvieron de base a la Ley de
5 la Gravitación Universal de
−3 3 Newton.
tanθ = ⇒ tanθ =
–3 −4 4
(–4; –3)
Matemática 1 - Secundaria 255