Page 258 - Matematica 1° Sec
P. 258
Capítulo 24
Razones trigonométricas de
ángulos de cualquier medida II
SIGNOS DE LAS RAZONES TRIGONOMÉTRICAS
Y
¿La R.T. de un ángulo
¿En qué cuadrantes negativo es siempre
el seno es negativo? negativo?
X
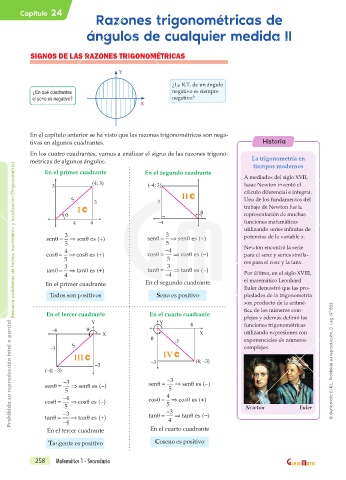
En el capítulo anterior se ha visto que las razones trigonométricas son nega-
tivas en algunos cuadrantes. Historia
En los cuatro cuadrantes, vamos a analizar el signo de las razones trigono-
métricas de algunos ángulos. La trigonometría en
Resuelve problemas de forma, movimiento y localización (Trigonometría)
tiempos modernos
En el primer cuadrante En el segundo cuadrante
A mediados del siglo XVII,
(4; 3) Isaac Newton inventó el
3 (–4; 3)
II C cálculo diferencial e integral.
5 3 3 Uno de los fundamentos del
I C trabajo de Newton fue la
representación de muchas
4 4 –4 funciones matemáticas
utilizando series infinitas de
3 3
θ
θ
senθ = ⇒ sen es + () senθ = ⇒ sen es + () potencias de la variable x.
5 5
4 −4 Newton encontró la serie
θ
θ
cosθ = ⇒ cos es + () cosθ = ⇒ cos es − () para el senx y series simila-
5 5 res para el cosx y la tanx.
3 3
tanθ = ⇒ tan es + () tanθ = ⇒ tan es − ()
θ
θ
4 −4 Por último, en el siglo XVIII,
En el primer cuadrante En el segundo cuadrante el matemático Leonhard
Euler demostró que las pro-
Todos son positivos Seno es positivo piedades de la trigonometría
son producto de la aritmé-
tica de los números com-
En el tercer cuadrante En el cuarto cuadrante plejos y además definió las
Y Y 4 funciones trigonométricas
Prohibida su reproducción total o parcia l
–4
X X utilizando expresiones con
5 exponenciales de números
5
–3 complejos.
III C IV C
–3 –3 (4; –3) Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
(–4; –3)
−3 senθ = −3 ⇒ sen es − ()
θ
θ
senθ = ⇒ sen es − () 5
5
−4 4
θ
cosθ = ⇒ cos es − () cosθ = ⇒ cos es +()
θ
5 5 Newton Euler
−3 tanθ = −3 ⇒ tan es −()
θ
tanθ = ⇒ tan es + () 4
θ
−4
En el tercer cuadrante En el cuarto cuadrante
Tangente es positivo Coseno es positivo
258 Matemática 1 - Secundaria