Page 23 - NUMINO TG_6A
P. 23
Activity 1 Find the LCM
jOb ective Find the least common multiple by prime factorization.
1. Textbook Instructions Activity 1 Find the LCM
Explain to students that the least common Learn about prime factorization.
multiple can be discovered using either of two
powerful methods. Prime factorization is writing a composite number as the product
of all of its factors that are prime numbers.
Method 1: Find the least common multiple of
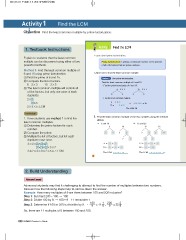
6 and 15 using prime factorization. Learn how to find the least common multiple.
Find the prime of 6 and 15. Method 1 Use prime factorization.
Compare the list of factors.
6 2 3 15 3 5 Find the least common multiple of 6 and 15.
The least common multiple will contain all Find the prime factorization of 6 and 15.
of the factors, but only one case of each
duplicate. 6=2 3 15 = 3 5
23
2335
35
2 3 5: LCM Find the least common multiple.
1. Have students use method 1 to find the 6 =2 3 2 3 5 = 30
least common multiples.
15 = 35
Determine the prime factors for each
number. The LCM: 30
Compare the prime.
Multiply the list of factors, but list each 1 . Find the least common multiple of the two numbers using the method
duplicate case once.
32332 above.
33257 a. 6 and 18 b. 12 and 26 26
3 2 3 3 2 5 7: LCM 6 18 12
2 33 6 2 62 13
2 3 2 3
23
6= 2 3 12 = 2 13
26 = 2
18 = 2 3 3
The LCM: 2 3 3 = 18 The LCM: 2 2 3 13 = 156
4
2. Build Understanding
Advanced students may find it challenging to attempt to find the number of multiples between two numbers.
Discuss how the following steps help to narrow down the answer.
Example: How many multiples of 9 are there between 100 and 200 inclusive?
Step 1: Subtract 200 100. 100
Step 2: Divide 100 by 9. 100 9 11 remainder 1
Step 3: Determine if 100 or 200 is divisible by 9. 100 11 1 , 200 22 2
9 9 9 9
So, there are 11 multiples of 9 between 100 and 200.
006 NUMINO Teacher s Guide
jOb ective Find the least common multiple by prime factorization.
1. Textbook Instructions Activity 1 Find the LCM
Explain to students that the least common Learn about prime factorization.
multiple can be discovered using either of two
powerful methods. Prime factorization is writing a composite number as the product
of all of its factors that are prime numbers.
Method 1: Find the least common multiple of
6 and 15 using prime factorization. Learn how to find the least common multiple.
Find the prime of 6 and 15. Method 1 Use prime factorization.
Compare the list of factors.
6 2 3 15 3 5 Find the least common multiple of 6 and 15.
The least common multiple will contain all Find the prime factorization of 6 and 15.
of the factors, but only one case of each
duplicate. 6=2 3 15 = 3 5
23
2335
35
2 3 5: LCM Find the least common multiple.
1. Have students use method 1 to find the 6 =2 3 2 3 5 = 30
least common multiples.
15 = 35
Determine the prime factors for each
number. The LCM: 30
Compare the prime.
Multiply the list of factors, but list each 1 . Find the least common multiple of the two numbers using the method
duplicate case once.
32332 above.
33257 a. 6 and 18 b. 12 and 26 26
3 2 3 3 2 5 7: LCM 6 18 12
2 33 6 2 62 13
2 3 2 3
23
6= 2 3 12 = 2 13
26 = 2
18 = 2 3 3
The LCM: 2 3 3 = 18 The LCM: 2 2 3 13 = 156
4
2. Build Understanding
Advanced students may find it challenging to attempt to find the number of multiples between two numbers.
Discuss how the following steps help to narrow down the answer.
Example: How many multiples of 9 are there between 100 and 200 inclusive?
Step 1: Subtract 200 100. 100
Step 2: Divide 100 by 9. 100 9 11 remainder 1
Step 3: Determine if 100 or 200 is divisible by 9. 100 11 1 , 200 22 2
9 9 9 9
So, there are 11 multiples of 9 between 100 and 200.
006 NUMINO Teacher s Guide