Page 148 - Algebra

From the graph you can conclude:
• •
roots.
• •
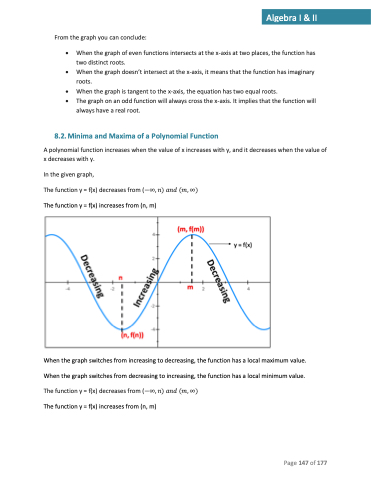
8.2. Minima and Maxima of a Polynomial Function
In the given graph,
The function y = f(x) decreases from (−∞, 𝑛) 𝑎𝑛𝑑 (𝑚, ∞) The function y = f(x) increases from (n, m)
When the graph switches from increasing to decreasing, the function has a local maximum value. When the graph switches from decreasing to increasing, the function has a local minimum value. The function y = f(x) decreases from (−∞, 𝑛) 𝑎𝑛𝑑 (𝑚, ∞)
The function y = f(x) increases from (n, m)
When the graph of even functions intersects at the x-axis at two places, the function has
two distinct roots.
When the graph doesn’t intersect at the x-axis, it means that the function has imaginary
When the graph is tangent to the x-axis, the equation has two equal roots.
The graph on an odd function will always cross the x-axis. It implies that the function will
always have a real root.
A polynomial function increases when the value of x increases with y, and it decreases when the value of
x decreases with y.
Page 147 of 177
Algebra I & II