Page 21 - NGTU_paper_withoutVideo

Modern Geomatics Technologies and Applications

( )
x ( ) (i) x (i + n) ≅ 0 , for all n, k ≠ l (8)

Where x (∎) (1023 + m) = x (∎) (m). The left side of Equation 8 defines the cross-correletion function of the the two
sequenses for shift n . The orthooghonality of these codes allowes all GNSS satillaties to broadcast simultananeouslely at the
same frequency without interfreing with each other [17].
The second important property is that a PRN seqence is nearly uncorrelated with itself, except forzero shift. for a C/A
code as Equation 9.

( )
x ( ) (i) x (i + n) ≅ 0 , for all |n| ≥ 1 (9)

The left-hand side of Equation 9 defines the auto-correlation function of a sequence for shift n. The auto-correlation
function of a PRN is nearly zero except for zero shift where it has a sharp peak. The cross-correletion and auto-correlation
function of a PRN are discussed numerically example in next section.
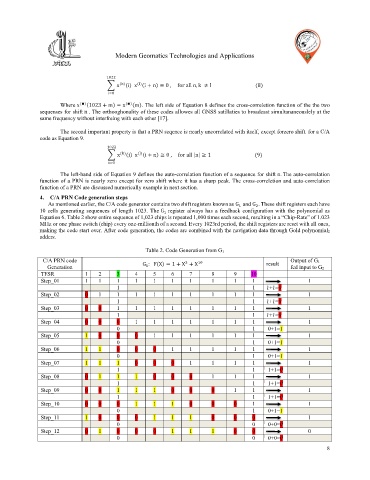
4. C/A PRN Code generation steps
As mentioned earlier, the C/A code generator contains two shift registers known as G and G . These shift registers each have
10 cells generating sequences of length 1023. The G register always has a feedback configuration with the polynomial as
Equation 6. Table 2 show entire sequence of 1,023 chips is repeated 1,000 times each second, resulting in a “Chip-Rate” of 1.023
MHz or one phase switch (chip) every one-millionth of a second. Every 1023rd period, the shift registers are reset with all ones,
making the code start over. After code generation, the codes are combined with the navigation data through Gold polynomial2
adders.

Table 2. Code Generation from G 1
C/A PRN code G : F(X) = 1 + X + X result Output of G 1

Generation fed input to G2
TFSR 1 2 3 4 5 6 7 8 9 10
Step_01 1 1 1 1 1 1 1 1 1 1 1
1 1 1+1=0
Step_02 0 1 1 1 1 1 1 1 1 1 1
1 1 1+1=0
Step_03 0 0 1 1 1 1 1 1 1 1 1
1 1 1+1=0
Step_04 0 0 0 1 1 1 1 1 1 1 1
0 1 0+1=1
Step_05 1 0 0 0 1 1 1 1 1 1 1
0 1 0+1=1
Step_06 1 1 0 0 0 1 1 1 1 1 1
0 1 0+1=1
Step_07 1 1 1 0 0 0 1 1 1 1 1
1 1 1+1=0
Step_08 0 1 1 1 0 0 0 1 1 1 1
1 1 1+1=0
Step_09 0 0 1 1 1 0 0 0 1 1 1
1 1 1+1=0
Step_10 0 0 0 1 1 1 0 0 0 1 1
0 1 0+1=1
Step_11 1 0 0 0 1 1 1 0 0 0 1
0 0 0+0=0
Step_12 0 1 0 0 0 1 1 1 0 0 0
0 0 0+0=0
8