Page 38 - KI - geometria 2 sec

Geometría 2° Secundaria

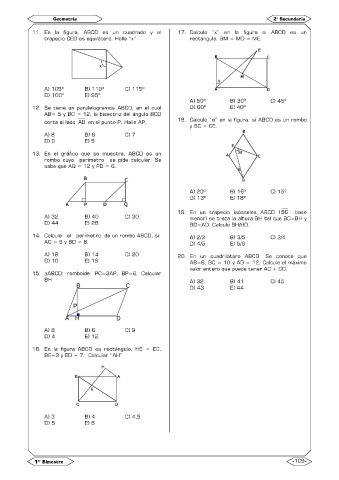
11. En la figura, ABCD es un cuadrado y el 17. Calcule “x” en la figura si ABCD es un
trapecio CED es equilátero. Halle “x” rectángulo. BM = MD = ME.

A) 105º B) 110º C) 115º
D) 100º E) 95º
A) 50º B) 30º C) 45º
12. Se tiene un paralelogramos ABCD, en el cuál D) 60º E) 40º
AB= 5 y BC = 12, la bisectriz del ángulo BCD
18. Calcule “α” en la figura, si ABCD es un rombo
corta al lado AD en el punto P. Halle AP.
y BC = CE.
A) 8 B) 6 C) 7
D) 9 E) 5

13. En el gráfico que se muestra, ABCD es un
rombo cuyo perímetro se pide calcular. Se
sabe que AQ = 12 y PD = 6.

A) 20º B) 16º C) 15º
D) 13º E) 18º

19. En un trapecio isósceles ABCD (BC : base
A) 32 B) 40 C) 30 menor) se traza la altura BH tal que BC=BH y
D) 44 E) 28 BD=AD. Calcule BH/HD.

14. Calcule el perímetro de un rombo ABCD, si A) 2/3 B) 3/5 C) 3/4
AC = 6 y BD = 8. D) 4/5 E) 5/6

A) 18 B) 14 C) 20 20. En un cuadrilátero ABCD. Se conoce que
D) 10 E) 16 AB=6, BC = 10 y AD = 12. Calcule el máximo
valor entero que puede tener AC + CD.
15. ABCD: romboide: PC=3AP, BP=6. Calcular
BH A) 32 B) 41 C) 45
D) 43 E) 44

A) 8 B) 6 C) 9
D) 4 E) 12

16. En la figura ABCD es rectángulo, HE = EC,
BE=3 y ED = 7. Calcular “AH”

A) 3 B) 4 C) 4,5
D) 5 E) 6

er
1 Bimestre -109-