Page 4 - Geometría 6

Geometría 6° Primaria

Propiedades
Dimensiones fundamentales
En los sólidos platónicos como en cualquier poliedro existe una serie de dimensiones que
es importante conocer. Éstas son: el área de la superficie y el volumen del sólido. Sea “a”
el tamaño de la arista de un sólido platónico. Entonces, veamos:

Poliedro Cubo Tetraedro Octaedro Dodecaedro Icosaedro
4 triángulos 8 triángulos 12 pentágonos 20 triángulos
Caras 6 cuadrados
equiláteros equiláteros regulares equiláteros
Vértices 8 4 6 20 12

Aristas 12 6 12 30 30

Poliedro Área de una Cara Área Total Apotema Volumen
a 2 a a 3
Tetraedro ⋅ 3 a 2 3 ⋅ 6 ⋅ 2
4 12 12
a 2 a a 3
Octaedro ⋅ 3 2a 2 3 ⋅ 6 ⋅ 2
4 6 3
a 2 a 7 3 5 5a 3 7 3 5
+
+
Icosaedro ⋅ 3 5a 2 3 ⋅ ⋅
4 2 6 6 2
a
2
3
2
Hexaedro a 6a a
2
+
5 5 2 5 5 2 5 a 25 11 5 5a 3 47 21 5
+
+
+
2
2
Dodecaedro a ⋅ 15a ⋅ ⋅ ⋅
2 5 5 2 10 2 10

Fórmula de Euler
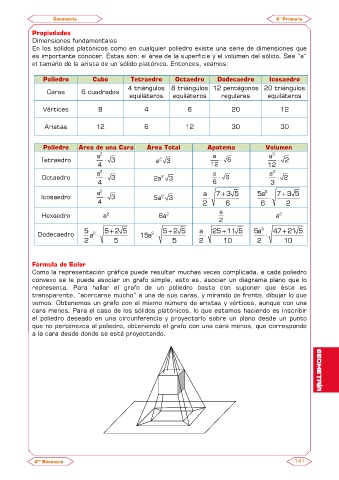
Como la representación gráfica puede resultar muchas veces complicada, a cada poliedro
convexo se le puede asociar un grafo simple, esto es, asociar un diagrama plano que lo
representa. Para hallar el grafo de un poliedro basta con suponer que éste es
transparente, “acercarse mucho” a una de sus caras, y mirando de frente, dibujar lo que
vemos. Obtenemos un grafo con el mismo número de aristas y vértices, aunque con una
cara menos. Para el caso de los sólidos platónicos, lo que estamos haciendo es inscribir
el poliedro deseado en una circunferencia y proyectarlo sobre un plano desde un punto
que no pertenezca al poliedro, obteniendo el grafo con una cara menos, que corresponde
a la cara desde donde se está proyectando.

to
4 Bimestre -141-