Page 5 - UNI III RAZONAMIENTO MATEMATICO SEC 5TO

Razonamiento Matemático 5° UNI

18
Semana

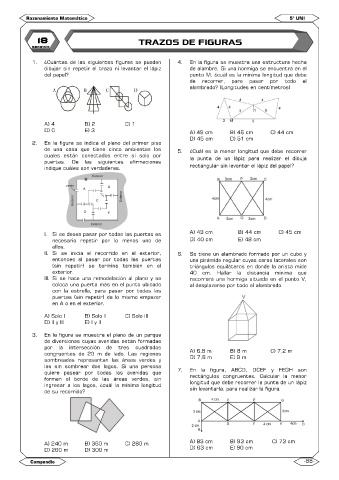
1. ¿Cuántas de las siguientes figuras se pueden 4. En la figura se muestra una estructura hecha
dibujar sin repetir el trazo ni levantar el lápiz de alambre. Si una hormiga se encuentra en el
del papel? punto M, ¿cuál es la mínima longitud que debe
de recorrer, para pasar por todo el
alambrado? (Longitudes en centímetros)

A) 4 B) 2 C) 1
D) 0 E) 3 A) 49 cm B) 46 cm C) 44 cm
D) 45 cm D) 51 cm
2. En la figura se indica el plano del primer piso
de una casa que tiene cinco ambientes los 5. ¿Cuál es la menor longitud que debe recorrer
cuales están conectados entre sí solo por la punta de un lápiz para realizar el dibuja
puertas. De las siguientes afirmaciones
indique cuáles son verdaderas. rectangular sin levantar el lápiz del papel?

I. Si se desea pasar por todas las puertas es A) 43 cm B) 44 cm C) 45 cm
necesario repetir por lo menos uno de D) 40 cm E) 48 cm
ellos.
II. Si se inicia el recorrido en el exterior, 6. Se tiene un alambrado formado por un cubo y
entonces al pasar por todas las puertas una pirámide regular cuyas caras laterales son
(sin repetir) se termina también en el triángulos equiláteros en donde la arista mide
exterior. 40 cm. Hallar la distancia mínima que
III. Si se hace una remodelación al plano y se recorrerá una hormiga situada en el punto V,
coloca una puerta más en el punto ubicado al desplazarse por todo el alambrado.
con la estrella, para pasar por todas las
puertas (sin repetir) da lo mismo empezar
en A o en el exterior.

A) Solo I B) Solo II C) Solo III
D) II y III E) I y II

3. En la figura se muestra el plano de un parque
de diversiones cuyas avenidas están formadas
por la intersección de tres cuadrados
congruentes de 20 m de lado. Las regiones A) 6,8 m B) 8 m C) 7,2 m
sombreadas representan las áreas verdes y D) 7,6 m E) 9 m
las sin sombrear dos lagos. Si una persona
quiere pasear por todas las avenidas que 7. En la figura, ABCD, DCEF y FEGH son
forman el borde de las áreas verdes, sin rectángulos congruentes. Calcular la menor
ingresar a los lagos, ¿cuál la mínima longitud longitud que debe recorrer la punta de un lápiz
de su recorrido? sin levantarla, para realizar la figura.

A) 240 m B) 360 m C) 280 m A) 83 cm B) 93 cm C) 73 cm
D) 260 m D) 300 m D) 63 cm E) 90 cm

Compendio -88-