Page 26 - SM Trigonometria 5to sec

Trigonometría 5° San Marcos

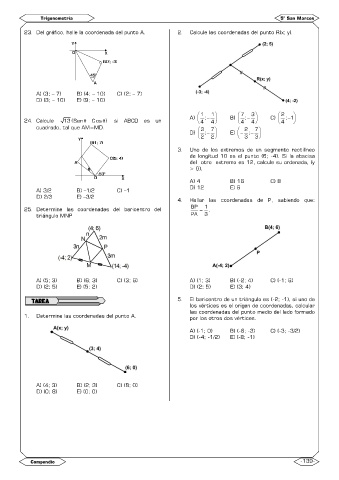
23. Del gráfico, halle la coordenada del punto A. 2. Calcule las coordenadas del punto R(x; y).

A) (3; – 7) B) (4; – 10) C) (2; – 7)
D) (3; – 10) E) (9; – 10)

 1 1  7 3   2 
24. Calcule 13 (Sen  − Cos )  si ABCD es un A)   4 ;− 4   B)   4 ;− 4   C)   4 ; 1  − 
cuadrado, tal que AM=MD.  3 7   2 7 
D)  ;−  E) −  ;− 
 2 2   3 3 

3. Uno de los extremos de un segmento rectilíneo
de longitud 10 es el punto (6; -4). Si la abscisa
del otro extremo es 12, calcule su ordenada, (y
> 0).

A) 4 B) 16 C) 8

A) 3/2 B) –1/2 C) –1 D) 12 E) 6
D) 2/3 E) –3/2
4. Hallar las coordenadas de P, sabiendo que:
25. Determine las coordenadas del baricentro del BP = 1 .
triángulo MNP PA 3

A) (5; 3) B) (6; 3) C) (3; 6) A) (1; 3) B) (-2; 4) C) (-1; 6)
D) (2; 5) E) (5; 2) D) (2; 5) E) (3; 4)

5. El baricentro de un triángulo es (-2; -1), si uno de
los vértices es el origen de coordenadas, calcular
las coordenadas del punto medio del lado formado
1. Determine las coordenadas del punto A. por los otros dos vértices.

A) (-1; 0) B) (-6; -3) C) (-3; -3/2)
D) (-4; -1/2) E) (-8; -1)

A) (4; 3) B) (2; 3) C) (8; 0)
D) (0; 8) E) (0; 0)

Compendio -139-