Page 5 - รวมไฟล์PBL
P. 5
เนื่องจากของไหลอุดมคติไม่สามารถอัดตัวได้ ดังนั้น ความหนาแน่นจึงไม่เปลี่ยนแปลง แสดงว่า
=
1
2
จะได้ =
1 1
2 2
นั่นคือ = ค่าคงตัว (1)
้
่
สมการ (1) เรียกว่า สมการความตอเนื่อง (equation of continuity) ซึ่งสรุปเป็นใจความ ไดว่า
่
ู
่
่
ิ
ผลคณระหวางพื้นที่หน้าตัดกับอัตราเร็วของของไหลอุดมคต ไมวาจะอยู่ที่ต าแหน่งใดในหลอดการไหล จะ
มีค่าคงตัวเสมอ
ู
ผลคณ เรียกว่า อัตราการไหล (volume flow rate หรอ volume flux) มีหน่วยลกบาศก์
ื
ู
เมตรต่อวินาท ี
จากสมการ (1) จะเห็นว่าอัตราเร็วของของไหลแปรผกผนกับพื้นที่หน้าตดของหลอดการไหล นั่นคอ
ื
ั
ั
ี่
็
่
ถ้าพื้นทหน้าตดเลก อัตราเร็วจะมาก และถ้าพื้นทหน้าตดใหญ่ อัตราเร็วจะน้อย การท มีคาคงตว ทาให้
ั
ี่
ั
่
ั
ี่
สามารถอธิบายไดว่า บริเวณหลอดการไหลที่มีพื้นทหน้าตัดเล็ก เส้นกระแสจะใกลชิดกัน และเส้นกระแสจะอยู่
ี่
้
้
ห่างกันในบริเวณของหลอดการไหลทมีพื้นทหน้าตดใหญ่ ดวยเหตนี้ เมื่อระยะห่างระหว่างเสนกระแสลด
ี่
้
ั
ุ
ี่
้
อัตราเร็วของของไหลจะเพิ่ม และเมื่อระยะห่างระหว่างเส้นกระแสเพิ่ม อัตราเร็วของของไหลจะลด
สมการแบร์นูลลี
่
่
ู
้
ี่
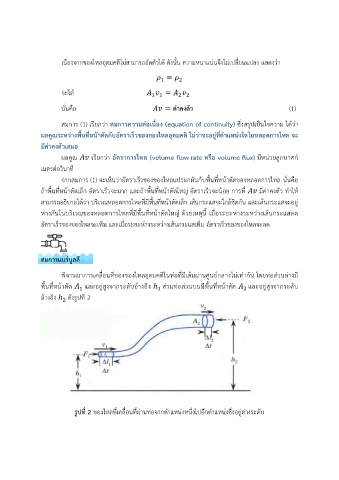
พิจารณาการเคลอนทของของไหลอุดมคตในทอทมีเสนผานศนย์กลางไม่เทากัน โดยทอสวนลางมี
่
่
่
ื่
ี่
ิ
่
ี่
ู
ั
ี่
ั
ั
ู
ั
่
พื้นทหน้าตด และอยู่สงจากระดบอ้างอิง ℎ สวนทอสวนบนมีพื้นทหน้าตด และอยู่สงจากระดบ
่
่
1
2
1
ี่
อ้างอิง ℎ ดังรูปท 2
2
ี่
รูปที่ 2 ของไหลที่เคลื่อนทผ่านท่อจากต่าแหน่งหนึ่งไปอีกต่าแหน่งซึ่งอยู่ต่างระดับ