Page 82 - u4

P2: OSO/OVY
P1: OSO/OVY
GO01962-Smith-v1.cls
UAE-Math-Grade-12-Vol-1-SE-718383-ch4
4-61 QC: OSO/OVY T1: OSO October 25, 2018 17:24 SECTION 4.7 • • Optimization 271
Notice that since x is a distance, we have x ≥ 0. Further, we have x ≤ 9, since
cutting squares of side 9 out of each corner will cut up the entire sheet of cardboard.
Thus, we are faced with finding the absolute maximum of the continuous function

V(x) = 4x(9 − x) 2
on the closed interval 0 ≤ x ≤ 9.
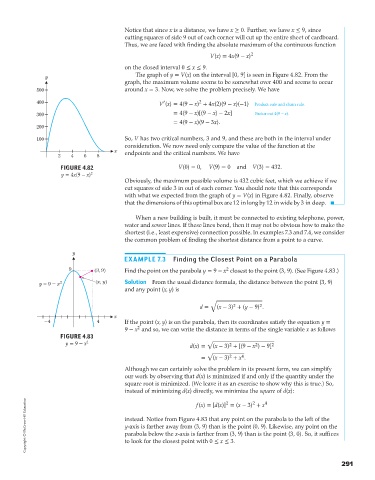
The graph of y = V(x) on the interval [0, 9] is seen in Figure 4.82. From the
y
graph, the maximum volume seems to be somewhat over 400 and seems to occur
500 around x = 3. Now, we solve the problem precisely. We have
′
2
400 V (x) = 4(9 − x) + 4x(2)(9 − x)(−1) Product rule and chain rule.
300 = 4(9 − x)[(9 − x) − 2x] Factor out 4(9 − x).
= 4(9 − x)(9 − 3x).
200

100 So, V has two critical numbers, 3 and 9, and these are both in the interval under
consideration. We now need only compare the value of the function at the
x endpoints and the critical numbers. We have
2 4 6 8

FIGURE 4.82 V(0) = 0, V(9) = 0 and V(3) = 432.
y = 4x(9 − x) 2
Obviously, the maximum possible volume is 432 cubic feet, which we achieve if we
cut squares of side 3 in out of each corner. You should note that this corresponds
with what we expected from the graph of y = V(x) in Figure 4.82. Finally, observe
that the dimensions of this optimal box are 12 in long by 12 in wide by 3 in deep.

When a new building is built, it must be connected to existing telephone, power,
water and sewer lines. If these lines bend, then it may not be obvious how to make the
shortest (i.e., least expensive) connection possible. In examples 7.3 and 7.4, we consider
the common problem of finding the shortest distance from a point to a curve.

y
EXAMPLE 7.3 Finding the Closest Point on a Parabola
2
9 (3, 9) Find the point on the parabola y = 9 − x closest to the point (3, 9). (See Figure 4.83.)
y = 9 - x 2 (x, y) Solution From the usual distance formula, the distance between the point (3, 9)
and any point (x, y) is

√
d = (x − 3) + (y − 9) .
2
2
x
-4 4 If the point (x, y) is on the parabola, then its coordinates satisfy the equation y =
2
9 − x and so, we can write the distance in terms of the single variable x as follows
FIGURE 4.83
y = 9 − x 2 d(x) = √ (x − 3) + [(9 − x ) − 9] 2
2
2
√
= (x − 3) + x .
4
2
Although we can certainly solve the problem in its present form, we can simplify
our work by observing that d(x) is minimized if and only if the quantity under the
square root is minimized. (We leave it as an exercise to show why this is true.) So,
instead of minimizing d(x) directly, we minimize the square of d(x):
Copyright © McGraw-Hill Education instead. Notice from Figure 4.83 that any point on the parabola to the left of the
2
4
2
f(x) = [d(x)] = (x − 3) + x
y-axis is farther away from (3, 9) than is the point (0, 9). Likewise, any point on the
parabola below the x-axis is farther from (3, 9) than is the point (3, 0). So, it suffices
to look for the closest point with 0 ≤ x ≤ 3.

291