Page 85 - u4

P1: OSO/OVY
GO01962-Smith-v1.cls
UAE-Math-Grade-12-Vol-1-SE-718383-ch4
CHAPTER 4 • •
Applications of Differentiation
274 P2: OSO/OVY QC: OSO/OVY T1: OSO October 25, 2018 17:24 4-64
We can eliminate one of the variables by using the fact that the volume (using
3
1floz ≈ 1.80469 in ) must be
3
2floz = 12 × 1.80469 = 21.65628 in .
Further, the volume of a right circular cylinder is

2
vol = r h
and so, h = vol ≈ 21.65628 . (7.3)
r 2 r 2
Thus, from (7.2) and (7.3), the surface area is approximately

(
2
2
A(r) = 2 r + 2 r 21.65628 = 2 r + 21.65628 ) .
r 2 r
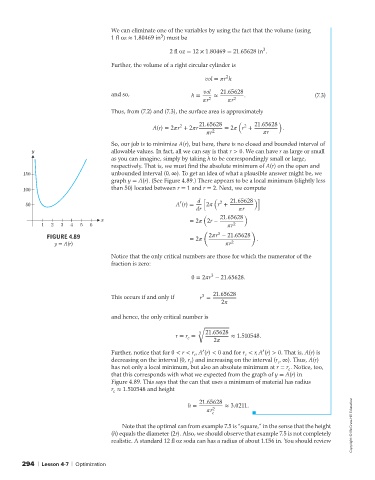
So, our job is to minimize A(r), but here, there is no closed and bounded interval of
y allowable values. In fact, all we can say is that r > 0. We can have r as large or small
as you can imagine, simply by taking h to be correspondingly small or large,
respectively. That is, we must find the absolute minimum of A(r) on the open and
150 unbounded interval (0, ∞). To get an idea of what a plausible answer might be, we
graph y = A(r). (See Figure 4.89.) There appears to be a local minimum (slightly less
100 than 50) located between r = 1 and r = 2. Next, we compute
(
2
′
50 A (r) = d [ 2 r + 21.65628 )]
dr r
( 21.65628 )
x = 2 2r −
1 2 3 4 5 6 r 2
( 3 )
FIGURE 4.89 = 2 2 r − 21.65628 .
y = A(r) r 2
Notice that the only critical numbers are those for which the numerator of the
fraction is zero:

3
0 = 2 r − 21.65628.

3
This occurs if and only if r = 21.65628
2
and hence, the only critical number is

√
r = r = 3 21.65628 ≈ 1.510548.
c
2
′
′
Further, notice that for 0 < r < r ,A (r) < 0 and for r < r, A (r) > 0. That is, A(r) is
c
c
decreasing on the interval (0, r ) and increasing on the interval (r , ∞). Thus, A(r)
c
c
has not only a local minimum, but also an absolute minimum at r = r . Notice, too,
c
that this corresponds with what we expected from the graph of y = A(r) in
Figure 4.89. This says that the can that uses a minimum of material has radius
r ≈ 1.510548 and height
c
h = 21.65628 ≈ 3.0211.
r 2 c
Note that the optimal can from example 7.5 is “square,” in the sense that the height Copyright © McGraw-Hill Education
(h) equals the diameter (2r). Also, we should observe that example 7.5 is not completely
realistic. A standard 12 fl oz soda can has a radius of about 1.156 in. You should review

294 | Lesson 4-7 | Optimization