Page 53 - CASA Bulletin 2022, 9(6) 增刊
P. 53
我的第二个创造性发现正是由于在上述自己提出的关于临界点的加权期望估计的算法中存在
一个瑕疵,它涉及到偏态分布中的期望估计。经过多年的冥思苦想和计算实践,一个有可能颠覆
统计学中关于连续型随机变量的期望估计的新算法于2010年12月12日在我的脑海中最终形成,
这就是为一个给定的连续型随机变量X {xi}(i = 1, 2, …, n )构造了一个相对简单、合理且有综合性
意义的权重W {wi }。这个权重依然是一个连续型随机变量。由于它的计算完全基于给定的连续型
随机变量X {xi },没有添加任何外来的数据或信息,因此,我称W {wi }为X {xi }的自权重。由于
W {wi }是一般权重的表示符号,为以示区别,将自权重改用C{ci }表示,一个ci表示的是第i个样本
点对抽样分布的未知中心期望的贡献(contribution)。于是,关于X {xi }的自加权期望估计的算法
可以形如一般加权均数的公式:
(1)
而在每个人都熟悉的算术均数的计算公式中,我们实际上默认了每个样本点对分布的中心期
望的贡献都相同,于是取ci = 1:
这就
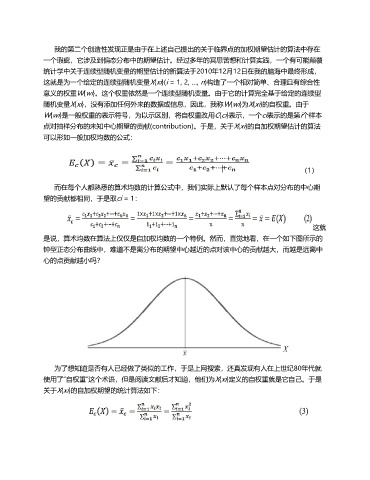
是说,算术均数在算法上仅仅是自加权均数的一个特例。然而,直觉地看,在一个如下图所示的
钟型正态分布曲线中,难道不是离分布的期望中心越近的点对该中心的贡献越大,而越是远离中
心的点贡献越小吗?
为了想知道是否有人已经做了类似的工作,于是上网搜索,还真发现有人在上世纪80年代就
使用了“自权重”这个术语,但是阅读文献后才知道,他们为X {xi }定义的自权重就是它自己。于是
关于X {xi }的自加权期望的统计算法如下: