Page 54 - CASA Bulletin 2022, 9(6) 增刊
P. 54
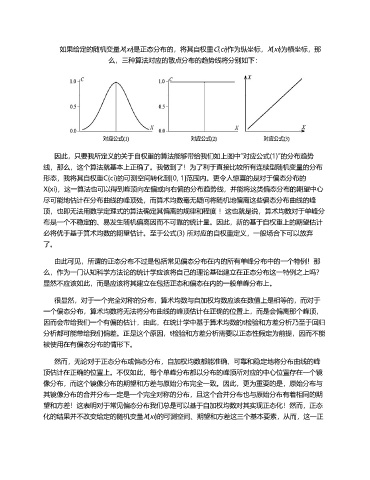
如果给定的随机变量X {xi }是正态分布的,将其自权重C{ci }作为纵坐标,X {xi }为横坐标,那
么,三种算法对应的散点分布的趋势线将分别如下:
因此,只要我所定义的关于自权重的算法能够带给我们如上图中“对应公式(1)”的分布趋势
线,那么,这个算法就基本上正确了。我做到了!为了利于直接比较所有连续型随机变量的分布
形态,我将其自权重C{ci}的可测空间转化到[0, 1]范围内。更令人惊喜的是对于偏态分布的
X{xi},这一算法也可以得到峰顶向左偏或向右偏的分布趋势线,并能将这类偏态分布的期望中心
尽可能地估计在分布曲线的峰顶处,而算术均数毫无疑问将随机地偏离这些偏态分布曲线的峰
顶,也即无法用数学定理式的算法确定其偏离的规律和程度 !这也就是说,算术均数对于单峰分
布是一个不稳定的、易发生随机偏离因而不可靠的统计量。因此,新的基于自权重上的期望估计
必将优于基于算术均数的期望估计。至于公式(3) 所对应的自权重定义,一般场合下可以放弃
了。
由此可见,所谓的正态分布不过是包括常见偏态分布在内的所有单峰分布中的一个特例!那
么,作为一门认知科学方法论的统计学应该将自己的理论基础建立在正态分布这一特例之上吗?
显然不应该如此,而是应该将其建立在包括正态和偏态在内的一般单峰分布上。
很显然,对于一个完全对称的分布,算术均数与自加权均数应该在数值上是相等的,而对于
一个偏态分布,算术均数将无法将分布曲线的峰顶估计在正确的位置上,而是会偏离那个峰顶,
因而会带给我们一个有偏的估计,由此,在统计学中基于算术均数的t检验和方差分析乃至于回归
分析都可能带给我们偏差。正是这个原因,t检验和方差分析需要以正态性假定为前提,因而不能
被使用在有偏态分布的情形下。
然而,无论对于正态分布或偏态分布,自加权均数都能准确、可靠和稳定地将分布曲线的峰
顶估计在正确的位置上。不仅如此,每个单峰分布都以分布的峰顶所对应的中心位置存在一个镜
像分布,而这个镜像分布的期望和方差与原始分布完全一致。因此,更为重要的是,原始分布与
其镜像分布的合并分布一定是一个完全对称的分布,且这个合并分布也与原始分布有着相同的期
望和方差!这表明对于常见偏态分布我们总是可以基于自加权均数对其实现正态化!然而,正态
化的结果并不改变给定的随机变量X {xi }的可测空间、期望和方差这三个基本要素,从而,这一正