Page 8 - HS 5 Algebraïsche functies in 3de graad

GeoGebra in de derde graad

In dit eerste voorbeeld is het mogelijk om de nulpunten langs algebraïsche weg te bepalen (met o.a. de
methode van Horner). Hou er mee rekening dat dit slechts mogelijk is bij goed gekozen voorbeelden.

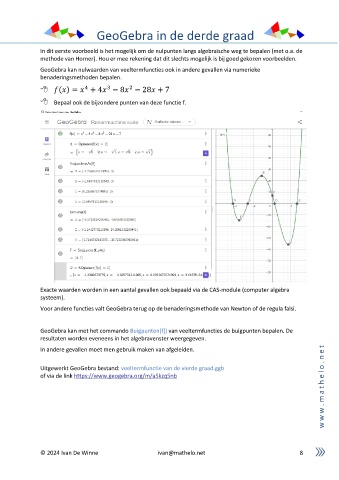
GeoGebra kan nulwaarden van veeltermfuncties ook in andere gevallen via numerieke
benaderingsmethoden bepalen.

3
4
2
 ( ) = + 4 − 8 − 28 + 7
 Bepaal ook de bijzondere punten van deze functie f.

Exacte waarden worden in een aantal gevallen ook bepaald via de CAS-module (computer algebra
systeem).
Voor andere functies valt GeoGebra terug op de benaderingsmethode van Newton of de regula falsi.

GeoGebra kan met het commando Buigpunten(f]) van veeltermfuncties de buigpunten bepalen. De
resultaten worden eveneens in het algebravenster weergegeven.

t
In andere gevallen moet men gebruik maken van afgeleiden.
e
n
.
Uitgewerkt GeoGebra bestand: veeltermfunctie van de vierde graad.ggb o
l
of via de link https://www.geogebra.org/m/a5kzq5nb e
h
t
a
m
.
w
w
w

© 2024 Ivan De Winne ivan@mathelo.net 8