Page 52 - Mathematics Coursebook

4.3 Reading scales

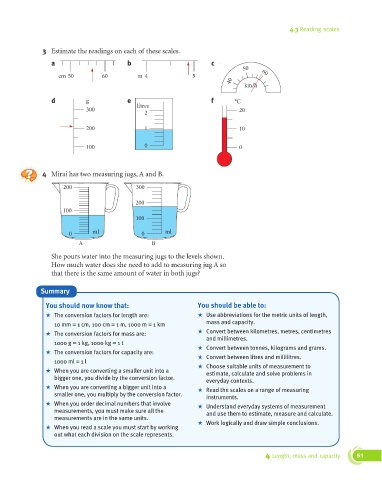
3 Estimate the readings on each of these scales.
50
a b c 50 50 60 60 60
50
cm cm 50 50 cm 50 60 60 60 m m 4 4 m 4 5 5 5 50 50 60
40
60
60
44
5050
cm 50 60 m 4 5 40 40 km/h km/h
cmcm
mm
6060
55
40km/h
40
40
km/hkm/h
km/h
d g g g e f °C °C °C
litres
°C°C
g
300
300 300 g g litres 2 litres 20 20 °C 20
2
lit 2
re
s
lit
300300 litresres 2020
300
20
2
22
200 200 200 1 1 1 10 10 10
200 11 1010
200200
1
10
100 100 100 0 0 0 0 0 0
0
100100 00 0
100
00
4 Mirai has two measuring jugs, A and B.
200 300
200
100
100
0 ml 0 ml
A B
She pours water into the measuring jugs to the levels shown.
How much water does she need to add to measuring jug A so
that there is the same amount of water in both jugs?
Summary
You should now know that: You should be able to:
+ The conversion factors for length are: + Use abbreviations for the metric units of length,
10 mm = 1 cm, 100 cm = 1 m, 1000 m = 1 km mass and capacity.
+ The conversion factors for mass are: + Convert between kilometres, metres, centimetres
and millimetres.
1000 g = 1 kg, 1000 kg = 1 t
+ Convert between tonnes, kilograms and grams.
+ The conversion factors for capacity are:
+ Convert between litres and millilitres.
1000 ml = 1 l
+ Choose suitable units of measurement to
+ When you are converting a smaller unit into a estimate, calculate and solve problems in
bigger one, you divide by the conversion factor. everyday contexts.
+ When you are converting a bigger unit into a + Read the scales on a range of measuring
smaller one, you multiply by the conversion factor. instruments.
+ When you order decimal numbers that involve + Understand everyday systems of measurement
measurements, you must make sure all the and use them to estimate, measure and calculate.
measurements are in the same units.
+ Work logically and draw simple conclusions.
+ When you read a scale you must start by working
out what each division on the scale represents.

4 Length, mass and capacity 4 Length, mass and capacity 51