Page 61 - Mathematics Coursebook

5.4 Solving angle problems

Section 5.4 Solving angle problems

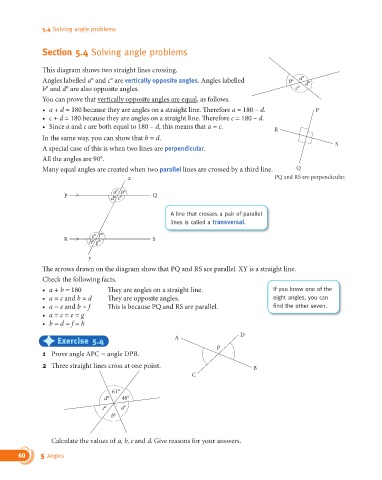
This diagram shows two straight lines crossing.
Angles labelled a° and c° are vertically opposite angles. Angles labelled b° a° d°
b° and d° are also opposite angles. c°
You can prove that vertically opposite angles are equal, as follows.
t a + d = 180 because they are angles on a straight line. $erefore a = 180 – d. P

t c + d = 180 because they are angles on a straight line. $erefore c = 180 – d.
t Since a and c are both equal to 180 – d, this means that a = c.
R
In the same way, you can show that b = d.
A special case of this is when two lines are perpendicular. S
All the angles are 90°.
Many equal angles are created when two parallel lines are crossed by a third line. Q
x PQ and RS are perpendicular.

a° b°
P d° c° Q

A line that crosses a pair of parallel
lines is called a transversal.
e° f°
R S
h° g°

y

$e arrows drawn on the diagram show that PQ and RS are parallel. XY is a straight line.
Check the following facts.
t a + b = 180 $ey are angles on a straight line. If you know one of the

t a = c and b = d $ey are opposite angles. eight angles, you can
t a = e and b = f $is is because PQ and RS are parallel. fi nd the other seven.

t a = c = e = g
t b = d = f = h

) Exercise 5.4 A D

P
1 Prove angle APC = angle DPB.
2 Three straight lines cross at one point. B
C

61°
d° 46°
c° a°
b°

Calculate the values of a, b, c and d. Give reasons for your answers.

60 5 Angles