Page 10 - E-MODULE TURUNAN FUNGSI ALJABAR
P. 10
E-MODULE Kelas XI
e
A. Pengertian Turunan
Permasalahan
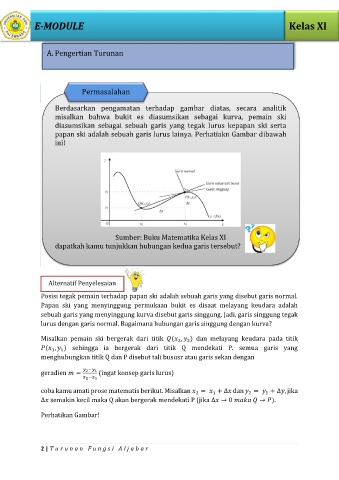
Berdasarkan pengamatan terhadap gambar diatas, secara analitik
misalkan bahwa bukit es diasumsikan sebagai kurva, pemain ski
diasumsikan sebagai sebuah garis yang tegak lurus kepapan ski serta
papan ski adalah sebuah garis lurus lainya. Perhatiakn Gambar dibawah
ini!
Sumber: Buku Matematika Kelas XI
dapatkah kamu tunjukkan hubungan kedua garis tersebut?
Alternatif Penyelesaian
Posisi tegak pemain terhadap papan ski adalah sebuah garis yang disebut garis normal.
Papan ski yang menyinggung permukaan bukit es disaat melayang keudara adalah
sebuah garis yang menyinggung kurva disebut garis singgung. Jadi, garis singgung tegak
lurus dengan garis normal. Bagaimana hubungan garis singgung dengan kurva?
Misalkan pemain ski bergerak dari titik ( , ) dan melayang keudara pada titik
2
2
( , ) sehingga ia bergerak dari titik Q mendekati P. semua garis yang
1
1
menghubungkan titik Q dan P disebut tali bususr atau garis sekan dengan
geradien = 2 − 1 (ingat konsep garis lurus)
2 − 1
coba kamu amati prose matematis berikut. Misalkan = + ∆ dan = + ∆ , jika
2
1
1
2
∆ semakin kecil maka Q akan bergerak mendekati P (jika ∆ → 0 → ).
Perhatikan Gambar!
2 | T u r u n a n F u n g s i A l j a b a r