Page 17 - Kelas XI_Fisika_KD 3.9

Modul Pembelajaran SMA/ Fisika Kelas XI

Dengan n = 0, 1, 2, 3, ….

Untuk menentukan letak simpul dari ujung bebas, Anda bisa menggunakan persamaan
berikut.

1
= λ(2n + 1) (9 – 14)
4

Dengan n = 0, 1, 2, 3, ….

2. Gelombang Stasioner Ujung Tetap

Bagaimana Anda bisa menurunkan persamaan gelombang stasioner ujung terikat?
Berbeda dengan gelombang stasioner ujung bebas, pada ujung tetap terjadi pembalikan
1
1
fase sebesar = sehingga beda fasenya menjadi ∆ =
2 2

3 2 1
1

1

2

3
2

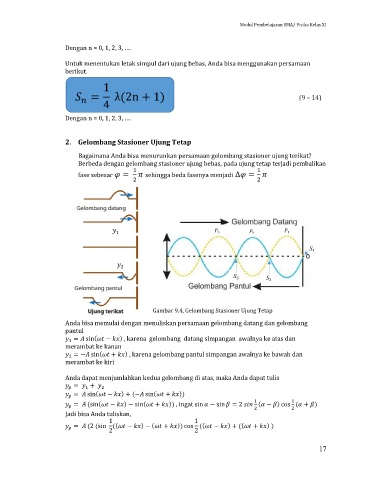
Gambar 9.4, Gelombang Stasioner Ujung Tetap

Anda bisa memulai dengan menuliskan persamaan gelombang datang dan gelombang
pantul
= sin( − ) , karena gelombang datang simpangan awalnya ke atas dan
1
merambat ke kanan
= − sin( + ) , karena gelombang pantul simpangan awalnya ke bawah dan
2
merambat ke kiri

Anda dapat menjumlahkan kedua gelombang di atas, maka Anda dapat tulis
= +

1
2
= sin( − ) + (− sin( + ))

1
1
= (sin( − ) − sin( + )) , ingat sin − sin = 2 ( − ) cos ( + )

2
2
Jadi bisa Anda tuliskan,
1 1
= (2 (sin (( − ) − ( + )) cos (( − ) + (( + ) )

2 2
17