Page 162 - mathematics 6'th

‫متوازي ا أل�ضلا ِع و�شب ُه المنحر ِف‬ ‫الدر� ُس ‪1‬‬

‫أتعلم‬ ‫فكر ُة الدر� ِس‬

‫توج ُد عند �سلي ٍم قطع َة أ�ر�ٍض على �شك ِل �شب ِه‬ ‫أ�تعر ُف خ�صائ�َص كل‬
‫منحر ٍف‪ ،‬ويوج ُد أ�ما َمها حديقة على �شك ِل‬ ‫من متوازي الأ�ضلاع‬
‫متوازي أ��ضلا ٍع‪ .‬كيف يمكنني �أن �أتعر َف على‬ ‫و�شبه المنحرف من حيث‬
‫خ�صائ�ِص كل من هذين ال�شكلي ِن من حيث‬ ‫الأ�ضلاع والزوايا‪.‬‬

‫الأ�ضلاع والزوايا ؟‬ ‫��قمااسشتلابعومُقهداافتازارل�شيدم�بانشاهب ُح ألتهارلا�لمضنفلمانح ِعحرر ِف ِف‬

‫يمكنني ت�صني ُف الا�شكال الرباعية وفق ًا لخ�صائ�ِص أ��ضلاعها وزواياها‬

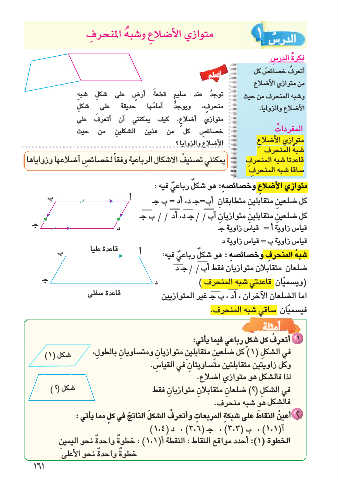
‫ب‬ ‫�أ‬ ‫متوازي ا أل�ضلا ِع وخ�صائ�ص ِه‪ :‬هو �شك ٌل رباع ٌي فيه ‪:‬‬
‫جـ‬ ‫كل �ضلعي ِن متقابلي ِن متطابقا ِن �أب=جـ د‪ ,‬أ�د = ب جـ‬
‫كل �ضلعي ِن متقابلي ِن متوازيا ِن أ�ب‪//‬جـ د‪� ,‬أد ‪ //‬ب جـ‬
‫ب‬ ‫قيا�س زاوية أ� = قيا�س زاوية جـ د‬
‫جـ‬ ‫قيا�س زاوية ب = قيا�س زاوية د‬
‫قاعدة عليا‬ ‫أ�‬
‫��شضبل ُهعاالنمنمحترقا ِبفلاونخم�تصاوائز�يصا ِهن‪:‬فهقوط�أ�شكب ٌل‪/‬ر‪/‬باجعـ ٌيدفيه‪:‬‬
‫(وي�سم ّيان قاعدتي �شبه المنحرف ) د‬
‫قاعدة �سفلى‬ ‫اما ال�ضلعان ا آلخران ‪� ,‬أد ‪ ,‬ب جـ غير المتوازيين‬

‫في�سم ّيان �ساقي �شبه المنحرف‪.‬‬
‫ا ألأمثـللـةة‬
‫ي�أتي‪:‬‬ ‫رباعي فيما‬ ‫�(ش‪1‬ك ٍ)ل‬ ‫�أتعر ُف كل‬ ‫‪1‬‬
‫�شكل (‪)1‬‬ ‫بالطو ِل‪,‬‬ ‫ومت�ساويا ِن‬ ‫متوازيا ِن‬
‫متقابلي ِن‬ ‫كل �ضلعي ِن‬ ‫في ال�شك ِل‬
‫وكل زاويتين متقابلتين مت�ساويتا ِن في القيا� ِس‪.‬‬
‫لذا فال�شكل هو متوازي ا�ضلاع‪.‬‬
‫�شكل (‪)2‬‬ ‫في ال�شك ِل (‪� )2‬ضلعا ِن متقابلا ِن متوازيا ِن فقط‬
‫فال�شكل هو �شبه منحرف‪.‬‬
‫‪2:‬‬
‫ي أ�تي‬ ‫مما‬ ‫ك ٍل‬ ‫في‬ ‫النات َج‬ ‫المربعا ِت و أ�تعر ُف ال�شك َل‬ ‫على �شبك ِة‬ ‫أ�عي ُن النقا َط‬

‫‪ ,‬جـ (‪ , )3,6‬د (‪)1,4‬‬ ‫ب (‪)3,3‬‬ ‫أ�(‪, )1,1‬‬
‫الخطوة (‪� :)1‬أحدد مواقع النقاط ‪ :‬النقطة أ�(‪ : )1,1‬خطو ٌة واحد ٌة نحو اليمي ِن‬
‫خطو ٌة واحد ٌة نحو الأعلى‬
‫‪161‬‬