Page 77 - YORAM RUDY BOOK FINAL

P. 77

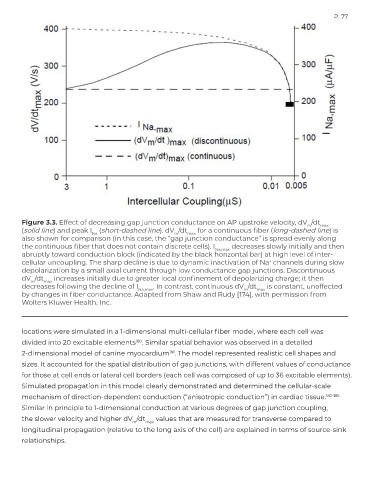
Figure 3.3. Effect of decreasing gap junction conductance on AP upstroke velocity, dV /dt max
m
(solid line) and peak I (short-dashed line). dV /dt max for a continuous fiber (long-dashed line) is
m
Na
also shown for comparison (in this case, the “gap junction conductance” is spread evenly along
the continuous fiber that does not contain discrete cells). I Na,max decreases slowly initially and then
abruptly toward conduction block (indicated by the black horizontal bar) at high level of inter-
cellular uncoupling. The sharp decline is due to dynamic inactivation of Na channels during slow
+
depolarization by a small axial current through low conductance gap junctions. Discontinuous
dV /dt max increases initially due to greater local confinement of depolarizing charge; it then
m
decreases following the decline of I Na,max . In contrast, continuous dV /dt max is constant, unaffected
m
by changes in fiber conductance. Adapted from Shaw and Rudy [174], with permission from
Wolters Kluwer Health, Inc.

locations were simulated in a 1-dimensional multi-cellular fiber model, where each cell was

divided into 20 excitable elements . Similar spatial behavior was observed in a detailed
180
2-dimensional model of canine myocardium . The model represented realistic cell shapes and
181
sizes. It accounted for the spatial distribution of gap junctions, with different values of conductance
for those at cell ends or lateral cell borders (each cell was composed of up to 36 excitable elements).

Simulated propagation in this model clearly demonstrated and determined the cellular-scale
mechanism of direction-dependent conduction (“anisotropic conduction”) in cardiac tissue. 182-185
Similar in principle to 1-dimensional conduction at various degrees of gap junction coupling,
the slower velocity and higher dV /dt max values that are measured for transverse compared to
m
longitudinal propagation (relative to the long axis of the cell) are explained in terms of source-sink
relationships.