Page 40 - 23966

48

k 
םייקמ הלש עובקהש
,
תינומרה העונת לאכ וז העונתל סחייתהל ןתינ ןכלו
עובק אוה
.
,
L

L
 
x
sin
 
:
לוקשה חוכה תאוושמב ולא םירשק ביצנ
x


תיווזה רשאכ
 .
L

L
x  
 
x 
2 L
תויטנגמו למשח ריצקת
2 L

וסוידרש
.
,
היהי תשקה ךרואש ירה
:

ה תדוקנל דע תלוקשמה השועש תשקה ךרוא
לגעמ ףקיה ךסמ תשקה לש יסחיה קלחה אוה לולסמה לש תיתחת
רטמטלוו
:

.
לולסמה תיתחתב תאצמנש
:
רטמרפמא

sin
 
mg
cos
mg


L

םימרזה קוח
:

:
םיחתמה קוח

,
ךנאל סחיב
תלוקשמהו
למשחו הקינכמ - הקיזיפתויטנגמו למשח ריצקת תויטנגמו למשח ריצקת V I למשחו הקינכמ - הקיזיפ םוכס © חתמ דדומה רישכמ םרז דדומה רישכמ לאיצנטופה דרומב םרוז דגנ לע םרזה : רטמטלוו אוה רוגס לגעמב םיחתמה םוכס 0 . ףוהכריק יקוח הדידמ ירישכמ ילאידיא : ילאידיא רטמרפמא : םרזה ןוויכב תולת אלל : ןהכ זראו ךברמ ודיעל תורומש תויוכזה לכ ב רטמרפמא  הנממ םיאצויה םימר
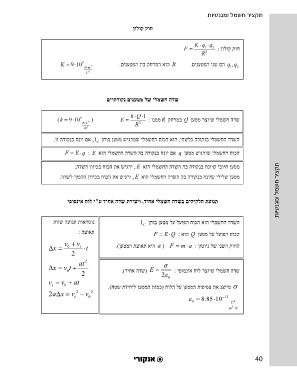
םינעטמ תכרעמ לש תילמשח היגרנא ןולוק קוח



U  Kq q 2 : םינעטמ ינשמ תבכרומה תכרעמ לש הי גרנאה F  Kq q 2 : ןולוק קוח
1
1
R R 2
. ינשהמ דחא R קחרמל , ףוסניאהמ םינעטמה תא איבהל השרדנש הדובעה איה היגרנאה K  9 10 9 . םינעטמה ן יב קחרמה אוה R . םינעטמה ינש םה qq
,

Nm 2 2 1 2
C

 Kq q
U total   r x y : םינעטמ רפסממ תבכרומה תכרעמ לש היגרנאה
, xy

.( םינעטמה תוגוז לכ ןיב תויגרנאה תא םימכוס )
םייתדוקנ םינעטמ לש ילמשח הדש
begin  U changes W U end : היגרנאה רומיש קוח kQ 1
k (  9 10 9 ) E   : ונממ R קחרמב Q ן עטמ רצויש ילמשח הדש

NC 2 R 2 #
ילמשחה לאיצנטופה m 2
. וז הדוקנב חנוי םא , 1 C ןחוב ןעטמ שיגרמש ילמשחה חוכה אוה , יהשלכ הדוקנב ילמשחה הדשה
םינעטמ רפסמ םירצויש ילמשחה לאיצנטופה q יתדוקנ ןעטמ רצויש ילמשחה לאיצנטופה
F  Eq : E אוה ילמשחה הדשה הב הדוקנב חנוי םא q ןעטמ שי גריש ילמשחה חוכה



V total   Kq x : םייתדוקנ V  Kq : ונממ R קחרמב
r
R
x
. הדשה ןוויכב חוכה תא שיגרי , E אוה ילמשחה הדשה הב הדוקנב חנויש יבויח ןעטמ
חנוישכ Q ןעטמ שיגריש תילמשחה היגרנאה אוה , יהשלכ הדוקנב ילמשחה לאיצנטופה . הדשל ךופהה ןוויכב חוכה תא שיגרי , E אוה ילמשחה הדשה הב הדוקנב חנויש ילילש ןעטמ
V : אוה לאיצנטופה הב הדוקנב 1 , C לש ןחוב ןעטמ שיגרמש תילמשחה היגרנאה תויטנגמו למשח ריצקת

U VQ . וז הדוקנב חנוישכ יפוסניא חול י " ע דיחא הדש תריציו , דיחא ילמשח הדשב םיקיקלח תעונת
: היגרנאה רומיש קוח רבעמב , Q ןעטמ דבאמ \ שכורש תילמשחה היגרנאה

תויטנגמו למשח ריצקת
begin  U changes W U end U  VQ : V םילאיצנטופ שרפה ןיב תווש העונת תואחסונ 1 C ןחוב ןעטמ לע לעופה חוכה אוה ילמשחה הדשה

: הצואת F  EQ : אוה Q ןעטמ לע לעופה חוכה



לאיצ נטופהו ילמשחה הדשה ןיב רשקה  v  v t t  .( ןעטמה תצואת איה a ) F  ma : ןוטוינ לש ינשה קוחה
x
0
2 2
חול רצויש ילמשח הדש E   V : לאיצנטופב יונישל ילמשחה הדשה ןיב רשקה  vt  at .( דיחא הדש ) E   : יפוסניא חול רצויש ילמשח הדש 23966-EYAL - 23966-EYAL | 3 - A | 18-01-11 | 16:57:34 | SR:-- | Magenta #23966-EYAL - 23966-EYAL | 3 - A | 18-01-11 | 16:57:34 | SR:-- | Yellow 23966-EYAL - 23966-EYAL | 3 - A | 18-01-11 | 16:57:34 | SR:-- | Black 23966-EYAL - 23966-EYAL | 3 - A | 18-01-11 | 16:57:34 | SR:-- | Cyan
x
X
0
E   : יפוסניא 2 2 0

2 0 U  VQ : ןעטמ דבאמ \ שכורש תילמשחה היגרנאה v  v  at .( חטש תדיחיל ןעטמ ה תו מכ ) חולה לע ןעטמה תופיפצ תא גציימ 
t
0
2
 0  8.85 10  12 C 2 2ax v  v 0 2   8.85 10  12
t
2
mN  V E X : עובק ילמשחה הדשה רשאכ 0 C 2 2


mN

ןהכ זראו ךברמ ודיעל תורומש תויוכזה לכ ©
ןהכ זראו ךברמ ודיעל תורומש תויוכזה לכ ©
41 40