Page 36 - 23966

44

r

Q

q 
)
(1
1

r
r



  
   
)
(1
  



1

0 r
0
0




0


/


 

B
A
TOTAL
R
2

E
E 

E
1
R
GMm
0

GM

B
E 

"
ע רצונה ילמשחה הדשה אוה

 
1

ןיוולה ךותב ףוג

1
ןרטקלאידה
תונפד לע םינעטמה תופיפצ
=
.

=
q
 
m
0


23966-EYAL - 23966-EYAL | 3 - A | 18-01-11 | 16:57:34 | SR:-- | Black
A
#23966-EYAL - 23966-EYAL | 3 - A | 18-01-11 | 16:57:34 | SR:-- | Yellow
N
E 
"

23966-EYAL - 23966-EYAL | 3 - A | 18-01-11 | 16:57:34 | SR:-- | Magenta
ע רצונה ילמשחה הדשה אוה
דבלב לבקה תוחול י
למרונה תא שיגרי ףוגה



.
=
לבקה תונפד לע םינעטמה תופיפצ
=


Q

.
בכוכה לש רוזחמה ןמז תא ול שיש ןמיס

TOTAL
תויטנגמו למשח ריצקת
E
,
ןכ ומכ
ןרטקלאידה ךותב ילמשחה הדשה
,


םיבושח םישגד
r

ןרטקלאידה ךותב ילמשחה הדשהש עודי
,

יפ ןטק

ןרטקלאידה תוצקב םירשומה םינעטמה בושיח

r
0
 
2
#
2

E 
R
3

1

3
d
C 
0
r

A
  
1

.
ןרטקלאידה אלל הדשהמ
R

r
 .
ב ןמוסמה ירטקלאיד םדקמ שי ירטקלאיד רמוח לכל

,
םינעטמ ויתוצקב םירבטצמ ךכמ האצותכ

.

לעמ םיגחה

למשחו הקינכמ - הקיזיפתויטנגמו למשח ריצקת ירטקלאיד רמוח ) תויטנגמו למשח ריצקת לבקה לע םינעטמה למשחו הקינכמ - הקיזיפ A E   יפ ןטק ןרטקלאידב הדשה r , ©  ןרטקלאיד r ( לבקה תוחול ןיב סנכומה דדובמ  . םילבקב ירטקלאיד רמוח  דבלב ןרטקלאידה תונפד י . ילמשחה הדשהמ ןרטקלאידה תוצק לע םירשומה םינעטמהו ילמשחה הדשה תא םינשמש , B Q ןהכ זראו ךברמ ודיעל תורומש תויוכזה לכ E q  לבקב   ,   . V חה תודשה לש לוקש אוה 
לבק לש הקירפו הניעט
םיניוול 3
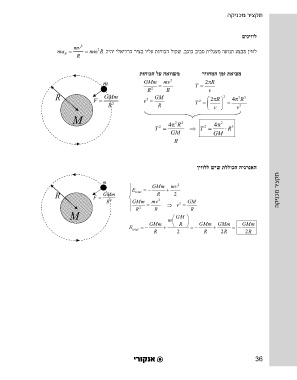
R C הניעט לגעמ ma  mv 2  m 2 R היהי ילאידרה ריצב וילע תוחוכה לוקש . בכוכ ביבס תילגעמ העונת עצבמ ןיוול
 R R
t  0, I  R : ינושארה עגרב
0

תוחוכה לע האוו שמ רוזחמה ןמז תאיצמ
GMm mv 2 2 R
 m  T 
R 2 R v
. הללוסה חתמל הוושו , עובק ראשנ ם מוכס לבא , םינתשמ לבקהו דגנה לש םיחתמה הניעטה ךלהמב R GMm GM 2

2
2
F  2 v  T   2 R    4 R 2
2
V  C V  R  R R   v   v 2
t M 2 2 2
 2 4 R 2 4 3
I  Ie RC : איה ןמזה לש היצקנופכ םרזה תכיעד תא תראתמה החסונה T  GM  T  GM  R
0
. והשלכ t ןמז רבעש רחאל דגנב םרזה אוה I R
0 . םה לבקה לע חתמהו ןעטמה וב , ינושארה עגרב םרזה אוה I 0

 יו ן ולל שיש תללוכה היגרנאה
I  : היהי , ןועט אל לבקהשכ , הניעטה לגעמב ינושארה םרזה ךרע
0
R
.( תוינשב דדמנ I ) אוה םרזה וב עגרל דע , I 0 היה םרזה וב עגרמ רבעש ןמזה קרפ אוה t m  E   GMm  mv 2

R GMm  total R 2 הקינכמ ריצקת
ןמז ךשמ לע " טלוש " הז ךרע . לבקה לש לוביקב דגנה לש תודגנתהה תלפכמ תא גציימ RC F  2  2
R  GMm  mv  v  2 GM
ןמסל גוהנ . לדג םרזה לש הכיעדה ןמז , לודג רתוי אוהש לככ . לגעמב םרזה לש הכיעדה  R 2 R R

M
.( תוינשב דדמנ ) " ןמזה עובק " תארקנ איהו ( ואט  ) תינוויה תואב RC הלפכמה תא m   GM  
תויטנגמו למשח ריצקת
E GMm  R  GMm GMm GMm
total   R  2   R  2R   2R
הקירפ לגעמ
V  V R : דגנה לע חתמל ןמזה לכ ההז לבקה לע חתמה
C

C Q
  ( לבקה לע t  0 עגרב ןעטמה אוה Q ) V  0 : ינושארה עגרב
  0 C C
 
  V
R I  R R : אוה ןותנ עגר לכב םרזה

t

I  Ie RC : החסונה התוא איה ןמזה לש היצקנופכ םרזה תכיעד תא תראתמה החסונה
0

ןהכ זראו ךברמ ודיעל תורומש תויוכזה לכ ©
45 36