Page 39 - Matematika-BS-KLS-XI_Neat
P. 39
⇣ ⌘
f f(x)
Pembagian dua fungsi g (x) = g(x) secara umum belum tentu menghasilkan
fungsi. Supaya f menjadi sebuah fungsi, pembagi g tidak boleh
g
memiliki nilai 0. Dengan kata lain, f adalah fungsi dengan domain
g
(D f ∩ D g ) − {x|g (x) = 0}.
Latihan 1.3
√
1. Jika f(x) = x + 3 dan g (x) = x + 3
a. Tentukan f (x) + g(x).
b. Tentukan domain dan range dari f (x) + g(x).
2
2. f(x) = x + 2 dan g (x) = 2x − 5
a. Tentukan f (x) − g(x).
b. Tentukan domain dan range dari f (x) − g(x).
3. Buatlah suatu fungsi kuadrat dan fungsi eksponensial! Tentukan hasil
penjumlahan dan pengurangan kedua fungsi tersebut!
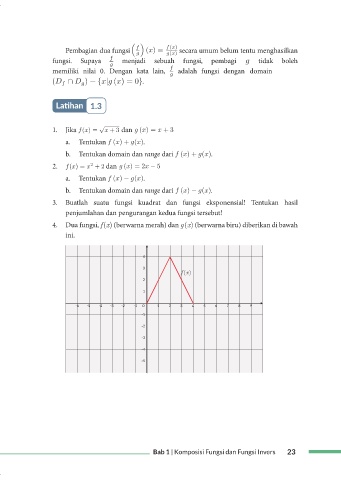
4. Dua fungsi, f(x) (berwarna merah) dan g(x) (berwarna biru) diberikan di bawah
ini.
4
3
f (x)
2
1
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9
-1
-2
-3
-4
-5
Bab 1 | Komposisi Fungsi dan Fungsi Invers 23