Page 235 - Withrow and MacEwen's Small Animal Clinical Oncology, 6th Edition

214 PART III Therapeutic Modalities for the Cancer Patient

tolerated, because without the treatment, patients may not live 10 1
long enough to develop late effects; however, for structures such S e 2
( D D )
as the spinal cord, where a late effect such as paralysis is viewed as
VetBooks.ir unacceptable, a 1% probability of effects is used. Conversely, for 10 0 S S at D /

procedures like SRT limb-sparing for canine osteosarcoma (OSA),
D
S e

the risk of fracture is affected by the region and condition of lytic for 0.15 Gy 1
bone at the time of treatment. Owners may choose to accept a
higher risk of fracture to maintain limb function, because a future
D
amputation can be used as a salvage procedure. 101 Surviving fraction 10 1 S e 2

It is not within the scope of this chapter to prescribe specific for 2
radiation doses or fractionation schedules, because many factors 0.03 Gy
must be considered. Rather, referring veterinarians must know 2

what to expect when sending patients to a radiation oncology 10 S S • S

center and should be able to explain the fundamental principles 2
D D
to clients. The radiation oncologist should inform the referring e
veterinarian and owner of the probabilities of tumor control, 10 3
acute effects, and late effects expected with a specific protocol. 0 2 4 6 8 10 12 14
The goal of RT is to destroy the reproductive capacity of the Dose (Gy)
tumor without excessive damage to surrounding normal tissues.
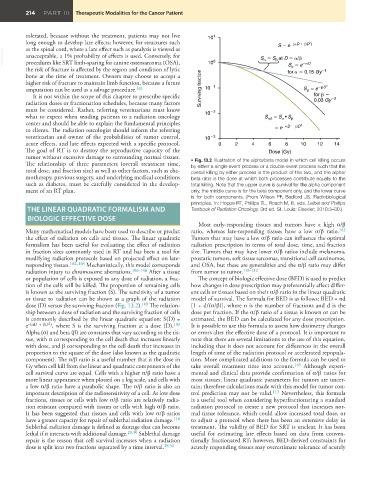
The relationship of three parameters (overall treatment time, • Fig. 13.2 Illustration of the alpha/beta model in which cell killing occurs
by either a single-event process or a double-event process such that the
total dose, and fraction size) as well as other factors, such as che- overall killing by either process is the product of the two, and the alpha/
motherapy, previous surgery, and underlying medical conditions beta ratio is the dose at which both processes contribute equally to the
such as diabetes, must be carefully considered in the develop- total killing. Note that the upper curve is survival for the alpha component
ment of an RT plan. only, the middle curve is for the beta component only, and the lower curve
is for both components. (From Wilson PF, Bedford JS. Radiobiological
principles. In: Hoppe RT, Phillips TL, Roach M, III, eds. Leibel and Phillips
THE LINEAR QUADRATIC FORMALISM AND Textbook of Radiation Oncology. 3rd ed. St. Louis: Elsevier; 2010:3–30.)
BIOLOGIC EFFECTIVE DOSE
Most early-responding tissues and tumors have a high α/β
Many mathematical models have been used to describe or predict ratio, whereas late-responding tissues have a low α/β ratio. 103
the effect of radiation on cells and tissues. The linear quadratic Tumors that may have a low α/β ratio can influence the optimal
formalism has been useful for evaluating the effect of radiation radiation prescription in terms of total dose, time, and fraction
in fraction sizes commonly used in RT and has been a tool for size. Tumors that may have lower α/β ratios include melanoma,
modifying radiation protocols based on projected effect on late- prostatic tumors, soft tissue sarcomas, transitional cell carcinomas,
responding tissues. 102–105 Mechanistically, this model corresponds and OSA, but these are generalities and the α/β ratio may differ
radiation injury to chromosome aberrations. 106–108 After a tissue from tumor to tumor. 110–112
or population of cells is exposed to any dose of radiation, a frac- The concept of biologic effective dose (BED) is used to predict
tion of the cells will be killed. The proportion of remaining cells how changes in dose prescription may preferentially affect differ-
is known as the surviving fraction (S). The sensitivity of a tumor ent cells or tissues based on their α/β ratio in the linear quadratic
or tissue to radiation can be shown as a graph of the radiation model of survival. The formula for BED is as follows: BED = nd
dose (D) versus the surviving fraction (Fig. 13.2). 109 The relation- [1 + d/(α/β)], where n is the number of fractions and d is the
ship between a dose of radiation and the surviving fraction of cells dose per fraction. If the α/β ratio of a tissue is known or can be
is commonly described by the linear quadratic equation: S(D) = estimated, the BED can be calculated for any dose prescription.
e –(αD + βD 2 ) , where S is the surviving fraction at a dose (D). 103 It is possible to use this formula to assess how dosimetry changes
Alpha (α) and beta (β) are constants that vary according to the tis- or errors alter the effective dose of a protocol. It is important to
sue, with α corresponding to the cell death that increases linearly note that there are several limitations to the use of this equation,
with dose, and β corresponding to the cell death that increases in including that it does not account for differences in the overall
proportion to the square of the dose (also known as the quadratic length of time of the radiation protocol or accelerated repopula-
component). The α/β ratio is a useful number that is the dose in tion. More complicated additions to the formula can be used to
Gy when cell kill from the linear and quadratic components of the take overall treatment time into account. 105 Although experi-
cell survival curve are equal. Cells with a higher α/β ratio have a mental and clinical data provide confirmation of α/β ratios for
more linear appearance when plotted on a log scale, and cells with most tissues, linear quadratic parameters for tumors are uncer-
a low α/β ratio have a parabolic shape. The α/β ratio is also an tain; therefore calculations made with this model for tumor con-
important description of the radiosensitivity of a cell. At low dose trol prediction may not be valid. 113 Nevertheless, this formula
fractions, tissues or cells with low α/β ratio are relatively radia- is a useful tool when considering hyperfractionating a standard
tion resistant compared with tissues or cells with high α/β ratio. radiation protocol to create a new protocol that increases nor-
It has been suggested that tissues and cells with low α/β ratios mal tissue tolerance, which could allow increased total dose, or
have a greater capacity for repair of sublethal radiation damage. 110 to adjust a protocol when there has been an extensive delay in
Sublethal radiation damage is defined as damage that can become treatment. The validity of BED for SRT is unclear. It has been
lethal if it interacts with additional damage. 29,30 Sublethal damage useful for estimating late effects based on data from conven-
repair is the reason that cell survival increases when a radiation tionally fractionated RT; however, BED-derived constraints for
dose is split into two fractions separated by a time interval. 29,30 acutely responding tissues may overestimate tolerance of acutely