Page 20 - Производная_Ф
P. 20
стационарной точке скорость изменения функции равна нулю, то есть функция ¾на мгнове-
ние¿ перестаёт меняться.
Стационарные точки могут быть трёх видов.
1. Точка максимума.
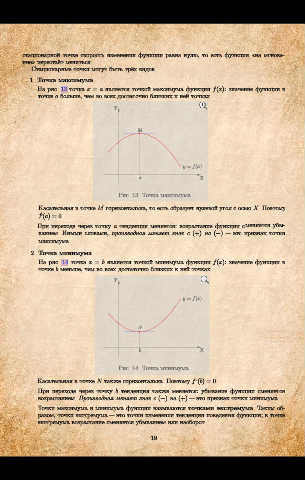
На рис. 13 точка x = a является точкой максимума функции f(x): значение функции в
точке a больше, чем во всех достаточно близких к ней точках.
Y
M
y = f(x)
a X
Рис. 13. Точка максимума
Касательная в точке M горизонтальна, то есть образует нулевой угол с осью X. Поэтому
0
f (a) = 0.
При переходе через точку a тенденция меняется: возрастание функции сменяется убы-
ванием. Иными словами, производная меняет знак с (+) на (−) это признак точки
максимума.
2. Точка минимума.
На рис. 14 точка x = b является точкой минимума функции f(x): значение функции в
точке b меньше, чем во всех достаточно близких к ней точках.
Y
y = f(x)
N
b X
Рис. 14. Точка минимума
0
Касательная в точке N также горизонтальна. Поэтому f (b) = 0.
При переходе через точку b тенденция также меняется: убывание функции сменяется
возрастанием. Производная меняет знак с (−) на (+) это признак точки минимума.
Точки максимума и минимума функции называются точками экстремума. Таким об-
разом, точки экстремума это точки изменения тенденции поведения функции; в точке
экстремума возрастание сменяется убыванием или наоборот.
19