Page 124 - mathematics first

Congruence Polygons تاعلضملا قباطت [ 5-5-2 ]

.يناثلا ثلثملا يف هل رظانم علضل قباطم لولاا ثلثملا يف علض لك ناك اذإ تاثلثملا قباطتت -
.اضيأ اياوزلا تاسايقو علاضلأا اهيف قباطتت نأ بجي علاضأ ةثلاث نم رثكا اهل يتلا لاكشلأا -
.امهنم يأ يف لوهجم علض لوط وا ةلوهجم ةيواز سايق عيطتسن ناعلضم قباطت اذإ -

A D ؟ ناقباطتم ناثلثملا له )3( لاثم

5cm 5cm
3cm 3cm

B 4cm C F 4cm E
AB =DE = 5cm

AC=DF=3cm
BC=EF=4cm يناثلا ثلثملا نم علض لك عم لولاا ثلثملا نم علض لك قباطتي

△ABC ≅ △DEF ناقباطتم نيثلثملا ناف اذل

؟يتلآا لكشلا يف ةلوهجملا ةيوازلا سايق دج )4( لاثم

66 ! 114 ! 114 ! ؟
امهاياوز تاسايق نأف نيقباطتم نيلكشلا نا امب
ً
! ! ! ةلوهجملا ةيوازلا سايق ناف اذل ، اضيأ ةقباطتم
114 66 ! 66 114
66 يواسي رواجملا لكشلا يف
O

Similarity هباشتلا ] 5-5-3 [

.~ هباشتلا زمر ،ةهباشتم اهنأب ةرظانتملا اهعلاضأ لاوطا يف بسانتتو هسفن لكشلا اهل يتلا لاكشلأل لاقي : هباشتلا
ً
. ةرظانتم اعلاضأ ةهباشتملا لاكشلأا يف علاضلأا ىمستو
. ةرظانتم اياوز ةهباشتملا لاكشلأا يف اياوزلا ىمستو

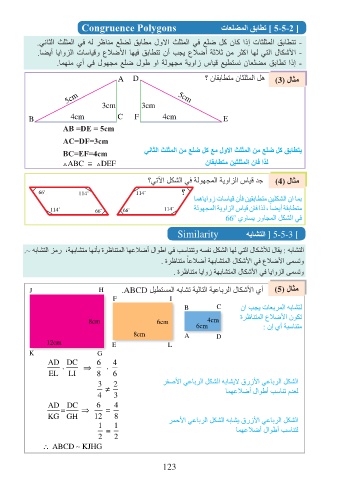
J H .ABCD ليطتسملا هباشت ةيلاتلا ةيعابرلا لاكشلأا يأ )5( لاثم
F I
B C نا بجي تاعبرملا هباشتل
ةرظانتملا علاضلأا نوكت
8cm 6cm 4cm
6cm : نإ يأ ةبسانتم
8cm A D
12cm E L

K G
AD AB 6 4
AD DC
= ⇒ =
,
= ,
EL
LI
ET EF 8 6
رفصلأا يعابرلا لكشلا هباشيلا قرزلأا يعابرلا لكشلا
3 2
≠ امهعلاضأ لاوطأ بسانت مدعل
4 3
AD DC
AD AB 6 4
= ⇒ =
=
KG KZ 12 8 رمحلأا يعابرلا لكشلا هباشي قرزلأا يعابرلا لكشلا
KG GH
1 1
= امهعلاضأ لاوطأ بسانتل
2 2
∴ ABCD ∼ KJHG
123