Page 23 - E-Modul Peluang Monica Silalahi

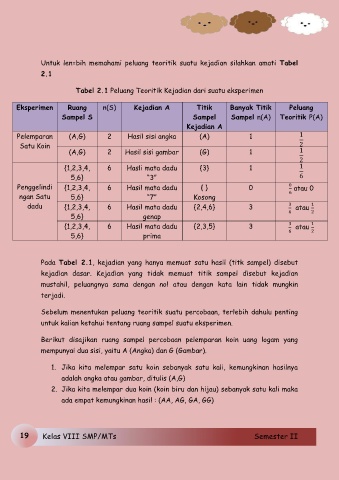
Untuk len=bih memahami peluang teoritik suatu kejadian silahkan amati Tabel
2.1

Tabel 2.1 Peluang Teoritik Kejadian dari suatu eksperimen

Eksperimen Ruang n(S) Kejadian A Titik Banyak Titik Peluang
Sampel S Sampel Sampel n(A) Teoritik P(A)

Kejadian A
Pelemparan (A,G) 2 Hasil sisi angka (A) 1
Satu Koin
(A,G) 2 Hasil sisi gambar (G) 1

{1,2,3,4, 6 Hasli mata dadu {3} 1
5,6} “3”
Penggelindi {1,2,3,4, 6 Hasil mata dadu { } 0 atau 0
ngan Satu 5,6} “7” Kosong
dadu {1,2,3,4, 6 Hasil mata dadu {2,4,6} 3 atau

5,6} genap
{1,2,3,4, 6 Hasil mata dadu {2,3,5} 3 atau

5,6} prima

Pada Tabel 2.1, kejadian yang hanya memuat satu hasil (titk sampel) disebut

kejadian dasar. Kejadian yang tidak memuat titik sampel disebut kejadian
mustahil, peluangnya sama dengan nol atau dengan kata lain tidak mungkin

terjadi.

Sebelum menentukan peluang teoritik suatu percobaan, terlebih dahulu penting

untuk kalian ketahui tentang ruang sampel suatu eksperimen.

Berikut disajikan ruang sampel percobaan pelemparan koin uang logam yang

mempunyai dua sisi, yaitu A (Angka) dan G (Gambar).

1. Jika kita melempar satu koin sebanyak satu kali, kemungkinan hasilnya

adalah angka atau gambar, ditulis (A,G)
2. Jika kita melempar dua koin (koin biru dan hijau) sebanyak satu kali maka

ada empat kemungkinan hasil : (AA, AG, GA, GG)

19 Kelas VIII SMP/MTs Semester II