Page 11 - MODUL MATEMATIKA 9
P. 11
TRANSFORMASI
Jawab:
A(-2, 1),
A(-2, 1),
ABC dengan koordinat titik
ABC dengan koordinat titik
4. Diketahui segitiga ABC dengan koordinat titik A(-2, 1), a. Bayangan titik Z oleh dilatasi terhadap pusat P(3, 2)
4. Diketahui segitiga ABC dengan koordinat titik A(-2, 1),
4. Diketahui segitiga
4. Diketahui segitiga
ABC didilatasikan terhadap
ABC didilatasikan terhadap
B(5, 1) dan C(1, 3). Segitiga
B(5, 1) dan C(1, 3). Segitiga ABC didilatasikan terhadap dengan faktor skala k = 3 adalah:
B(5, 1) dan C(1, 3). Segitiga ABC didilatasikan terhadap
B(5, 1) dan C(1, 3). Segitiga
titik O(0, 0) dengan faktor skala 2 sehingga diperoleh
titik O(0, 0) dengan faktor skala 2 sehingga diperoleh Bayangan titik T(x, y) oleh dilatasi dengan pusat rotasi P(a, b)
titik O(0, 0) dengan faktor skala 2 sehingga diperoleh
titik O(0, 0) dengan faktor skala 2 sehingga diperoleh
A
A
A
segitiga
segitiga A’B’C’.
segitiga
segitiga
’B’C’.
’B’C’.
’B’C’.
faktor skala k ® Rumus: [kx + (1 - k)a , ky + (1 - k)b ]
’, B’, dan C’.
A
A
’, B’, dan C’.
a. tentukan koordinat titik
a. tentukan koordinat titik A ’, B’, dan C’.
a. tentukan koordinat titik
a. tentukan koordinat titik A’, B’, dan C’.
BIDFORM
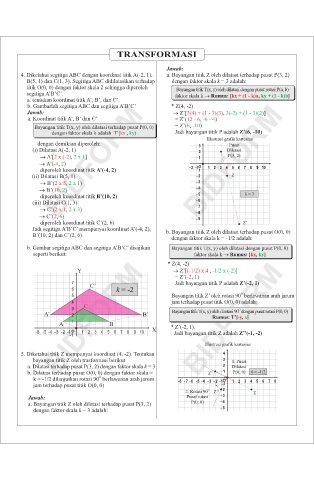
b. Gambarlah segitiga ABC dan segitiga A ’B’C’ * Z(4, -2)
b. Gambarlah segitiga ABC dan segitiga A’B’C’
ABC dan segitiga
ABC dan segitiga
b. Gambarlah segitiga
’B’C’
b. Gambarlah segitiga
’B’C’
A
A
Jawab:
Jawab:
Jawab:
Jawab: ® Z’[3(4) + (1 - 3)(3) , 3(-2) + (1 - 3)(2) ]
’, B’
’, B’
A
A
’, B’
A
a. Koordinat titik
a. Koordinat titik A’, B’ dan C’ = Z’(12 - 6 , -6 - 4 )
a. Koordinat titik
dan C’
a. Koordinat titik
dan C’
dan C’
6
Bayangan titik T(x, y) oleh dilatasi terhadap pusat P(0, 0) = Z’( , -10 )
dengan faktor skala k adalah T’[kx , ) Jadi bayangan titik P adalah Z’(6, -10)
ky
Illustrasi grafik kartesius
dengan demikian diperoleh:
dengan demikian diperoleh: Pusat
dengan demikian diperoleh:
dengan demikian diperoleh:
3
A(-2, 1)
A(-2, 1)
(i) Dilatasi
(i) Dilatasi A(-2, 1)
(i) Dilatasi
(i) Dilatasi A(-2, 1) 2 Dilatasi
’[
’[
® ® ® A ’[ 2 x (-2) , 2 x 1] 1 P(3, 2)
A
A
® A’[2 x (-2), 2 x 1]
2 x (-2)
2 x 1
2 x (-2)
,
,
2 x 1
]
]
2
2
A
2
®
®
®
-4
’(
’(
-4
-4
-4
’(
A
A
2
,
,
,
® A’( , ) ) ) ) BIDFORM
O
diperoleh koordinat titik
diperoleh koordinat titik A’(-4, 2)
diperoleh koordinat titik A ’(-4, 2) -2 -1 -1 1 2 3 4 5 6 7 8 9 10
diperoleh koordinat titik
’(-4, 2)
A
A
’(-4, 2)
(ii) Dilatasi B(5, 1)
(ii) Dilatasi B(5, 1) -2 Z
(ii) Dilatasi B(5, 1)
(ii) Dilatasi B(5, 1)
2 x 1
,
,
2 x 5
2 x 5
2 x 5
B’(
2 x 1
B’(
, 2 x 1)
B’(
)
)
® ® ®
® B’(2 x 5, 2 x 1) -3
2
®
2
®
®
B’(
B’(
B’(
10
10
10
10
2
2
,
,
,
® B’( , ) ) ) ) -4
diperoleh koordinat titik
diperoleh koordinat titik B’(10, 2) -5 k = 3
diperoleh koordinat titik
B’(10, 2)
B’(10, 2)
diperoleh koordinat titik B’(10, 2)
-6
(iii) Dilatasi C(1, 3)
(iii) Dilatasi C(1, 3)
(iii) Dilatasi C(1, 3)
(iii) Dilatasi C(1, 3)
-7
® ® ®
2 x 1
2 x 1
2 x 3
2 x 1
® C’(2 x 1, 2 x 3)
, 2 x 3)
C’(
C’(
,
,
)
2 x 3
C’(
)
-8
2
2
2
2
6
6
6
6
,
,
,
C’(
®
C’(
C’(
® C’( , ) ) ) )
®
®
-9
diperoleh koordinat titik C’(2, 6)
diperoleh koordinat titik C’(2, 6) Z’
diperoleh koordinat titik C’(2, 6)
diperoleh koordinat titik C’(2, 6)
’(-4, 2),
’(-4, 2),
mempunyai koordinat
A
Jadi segitiga
Jadi segitiga
A
Jadi segitiga A’B’C’ mempunyai koordinat A’(-4, 2),
Jadi segitiga A ’B’C’ mempunyai koordinat A ’(-4, 2), b. Bayangan titik Z oleh dilatasi terhadap pusat O(0, 0)
A
A
mempunyai koordinat
’B’C’
’B’C’
B’(10, 2) dan C’(2, 6)
B’(10, 2) dan C’(2, 6)
B’(10, 2) dan C’(2, 6)
B’(10, 2) dan C’(2, 6)
dengan faktor skala k = -1/2 adalah:
b. Gambar segitiga
ABC dan segitiga
disajikan
disajikan
disajikan
b. Gambar segitiga
b. Gambar segitiga ABC dan segitiga A’B’C’ disajikan Bayangan titik T(x, y) oleh dilatasi dengan pusat P(0, 0)
b. Gambar segitiga
ABC dan segitiga
ABC dan segitiga
’B’C’
’B’C’
A
A
A
’B’C’
seperti berikut:
seperti berikut:
seperti berikut:
seperti berikut: faktor skala k ® Rumus: [kx , ky ]
BIDFORM
BIDFORM
* Z(4, -2)
Y ® Z’[(-1/2) x 4 , -1/2 x (-2) ]
1
-2
= Z’( , )
7 Jadi bayangan titik P adalah Z’(-2, 1)
C’
6 k = -2
O
5 Bayangan titik Z’ oleh rotasi 90 berlawanan arah jarum
4 jam terhadap pusat titik O(0, 0) adalah:
C
3 O
A’ 2 B’ Bayangan titik T(x, y) oleh dirotasi 90 dengan pusat rotasi P(0, 0)
-y
Rumus: T’[ , ]
x
1
A B * Z’(-2, 1).
-6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6 7 8 9 10 X Jadi bayangan titik Z adalah Z’’(-1, -2)
-1
Illustrasi grafik kartesius
T
entukan
entukan
5. Diketahui titik Z mempunyai koordinat (4, -2). Tentukan
5. Diketahui titik Z mempunyai koordinat (4, -2).
5. Diketahui titik Z mempunyai koordinat (4, -2).
5. Diketahui titik Z mempunyai koordinat (4, -2). T entukan 4
T
bayangan titik Z oleh trasformasi berikut
bayangan titik Z oleh trasformasi berikut
bayangan titik Z oleh trasformasi berikut
bayangan titik Z oleh trasformasi berikut 3 1. Pusat
=
n
n
n
f
f
f
a
a
3
3
d
d
e
e
e
d
l
g
g
a
a
a
n
n
n
=
g
r
k
3
a
a
s
s
a
s
k
a
k
k
a a a
k
a. Dilatasi terhadap pusat P(3, 2) dengan faktor skala k = 3 2 Dilatasi
t
t
k
a
l
k
l
t
k
o
=
r
r
a
a
k
o
o
)
h
h
h
a
d
a
a
D
e
e
D
r
r
r
d
p
p
p
a
a
d
a
p
p
p
a
t
t
a
i
i
a
l
l
l
a
t
a
a
i
t
t
e
D
t
s
s
s
i
i
i
P
P
P
2
t
2
3
,
3
(
3
(
(
,
,
s
.
a
a
s
u
u
s
u
.
.
2
t
t
)
a
)
b. Dilatasi terhadap pusat O(0, 0) dengan faktor skala =
b. Dilatasi terhadap pusat O(0, 0) dengan faktor skala =
b. Dilatasi terhadap pusat O(0, 0) dengan faktor skala = Z’ 1 P(0, 0) k = -1/2
b. Dilatasi terhadap pusat O(0, 0) dengan faktor skala =
berlawanan arah jarum
berlawanan arah jarum
k = -1/2 dilanjutkan rotasi 90
k = -1/2 dilanjutkan rotasi 90 berlawanan arah jarum
k = -1/2 dilanjutkan rotasi 90 O O O O berlawanan arah jarum -8 -7 -6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6 7 8
k = -1/2 dilanjutkan rotasi 90
jam terhadap pusat titik O(0, 0)
jam terhadap pusat titik O(0, 0) -1
jam terhadap pusat titik O(0, 0)
jam terhadap pusat titik O(0, 0)
2. Rotasi 90 O Z’’ -2 Z
Jawab: Pusat rotasi -3
Jawab:
Jawab:
Jawab:
a. Bayangan titik Z oleh dilatasi terhadap pusat P(3, 2)
a. Bayangan titik Z oleh dilatasi terhadap pusat P(3, 2) P(0, 0) -4
a. Bayangan titik Z oleh dilatasi terhadap pusat P(3, 2)
a. Bayangan titik Z oleh dilatasi terhadap pusat P(3, 2)
dengan faktor skala k = 3 adalah:
= 3 adalah:
k
k
dengan faktor skala
dengan faktor skala
= 3 adalah:
dengan faktor skala k = 3 adalah: -5